
Electronique
> Réalisations
> Correcteurs
>
Filtre BF 008 (3 filtres différents)
Dernière mise à jour : 05/06/2009Présentation
Trois filtres actifs sont décrits ici et sont simples à construire. Ils sont de type suivant :- Filtre 008a : filtre passe-bas
- Filtre 008b : filtre passe-haut
- Filtre 008c : filtre passe-bande
Les trois filtres sont réunis sur la même page car bien que présentant des caractéristiques de filtrage différentes, ils sont basés sur la même structure de base.
La structure de base
La structure de base des trois filtres dont les schémas vont suivre, est donnée sur le schéma suivant.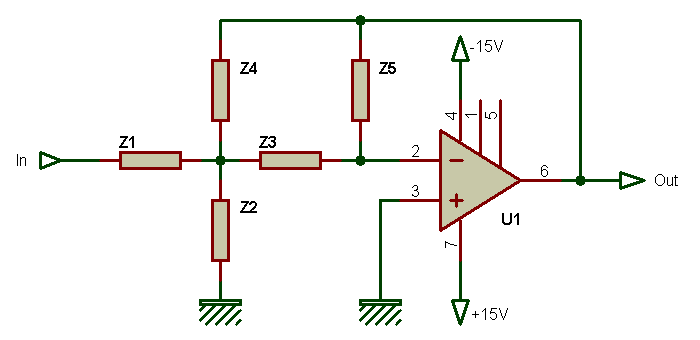
On y découvre un AOP et cinq composants nommés Z1 à Z5 (composants passifs de type résistance ou condensateur), que l'on peut voir pour certains comme faisant partie du circuit d'entrée ou comme élements de contre-réaction. Selon le type de composant que l'on met à la place de Z1 .. Z5, nous pouvons définir une fonction de transfert différente pour le circuit. Pour rappel, la fonction de transfert définie sous forme d'une formule mathématique la valeur de la tension de sortie, en fonction de la valeur de la tension d'entrée et de la valeur des composants utilisés dans la fonction de filtrage elle-même (ici Z1 à Z5). On retrouve dans ce type de configuration les avantages d'une impédance d'entrée élevée et d'une impédance de sortie faible, et éventuellement la possibilité de travailler avec un certain gain. Les trois filtres qui suivent se voient dotés des mêmes types de composants, c'est à dire résistances et condensateurs, dont l'emplacement définie précisement le type de filtre. Afin de garder un lien entre le schéma de base et les schémas qui suivent, les appellations Z1 à Z5 seront laissées entre parenthèses, à coté de la valeur des composants concernés.
Le schéma du filtre 008a - Passe-bas
Avant d'attaquer le filtre passe-bas actif 008a, un petit rappel
concernant le filtre passe-bas passif...Filtre passe-bas passif
Le filtre passe-bas le plus simple que l'on puisse concevoir est de type passif et comporte seulement deux composants : une résistance et un condensateur. Dans le schéma qui suit, les valeurs données aux composants sont arbitraires mais sont tout de même choisies de telle sorte que la fréquence de coupure se situe dans la bande audio.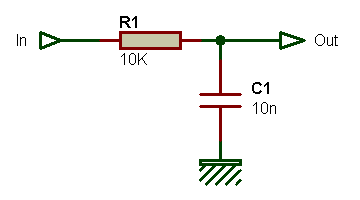
La réponse en fréquence de ce simple filtre de type "premier ordre" est semblable à la courbe suivante, la pente d'atténuation est de 6 dB par octave (amplitude électrique 2 fois moindre à chaque fois que l'on multiplie la fréquence par deux) à partir de la fréquence de coupure, qui dépend directement de la valeur donnée aux deux composants R et C.
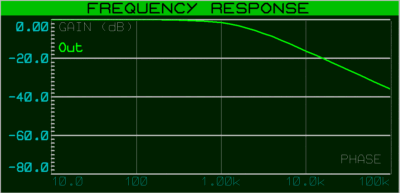
La pulsation w0 du filtre est définie par la formule suivante :
w0 = 1 / (R1 * C1)
La fréquence de coupure Fc (à -3 dB) quant à elle est définie par la formule suivante :
Fc = 1 / (2 * Pi * R1 * C1)
Ici, nous avons, avec R1 = 10 KO et C1 = 10 nF :
w0 = 1 / (10000 * 0,00000001) = 10000
Fc = 1 / (2 * Pi * 10000 * 0,00000001) = 1,59 KHz
Filtre passe-bas actif (008a)
Le filtre actif proposé à la suite est un peu
différent, puisqu'il emploie plus de résistances et de
condensateurs, et que l'on y trouve un composant actif, ici un AOP. Il
est appelé filtre à contre-réaction multiple car
la sortie se trouve rebouclée en plusieurs endroits de
l'entrée (il existe des filtres actifs à
contre-réaction simple où la sortie n'aboutit qu'à
un seul point du circuit d'entrée), et adopte la structure de
Rauch.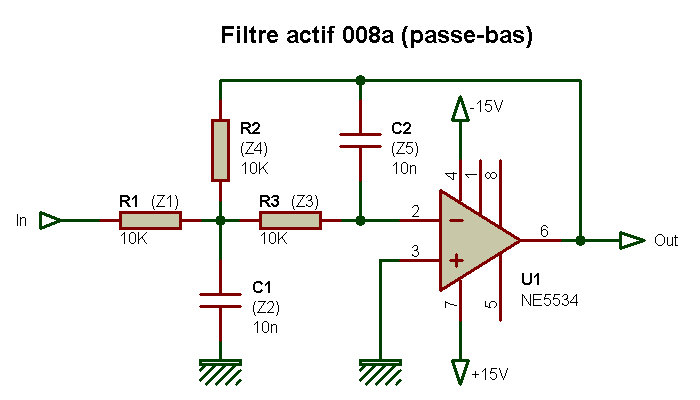
La réponse en fréquence de ce filtre actif de type "deuxième ordre" est semblable à la courbe suivante, la pente d'atténuation est cette fois de 12 dB par octave à partir de la fréquence de coupure (pente deux fois plus raide que celle du filtre passif vu avant, amplitude électrique 4 fois moindre à chaque fois que l'on multiplie la fréquence par deux).
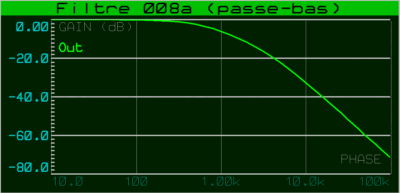
Fréquence de coupure
La fréquence de coupure dépend là encore directement de la valeur donnée aux composants R et C. Si les deux condensateurs ont même valeur (C) et si les trois résistances ont aussi même valeur (R), la pulsation w0 du filtre peut alors être représentée par une formule on ne peut plus simple, qui est identique à celle vue avec le filtre passe-bas passif précédent :w0 = 1 / (R * C)
Ce qui donne là encore pour la fréquence de coupure :
Fc = 1 / (2 * Pi * R * C)
Avec les valeurs du schéma, nous avons :
w0 = 1 / (10000 * 0,00000001) = 10000
Fc = 1 / (2 * Pi * 10000 * 0,00000001) = 1,59 KHz
Comme nous avons affaire à une fonction "linéaire", le fait de doubler la valeur des résistances ou des condensateurs a pour effet de baisser la fréquence de coupure dans un même rapport de deux. Si la fréquence de coupure est de 1,59 KHz avec des résistances de 10 KO et des condensateurs de 10 nF, alors elle sera de 3,2 KHz avec des résistances de 5 KO et des condensateurs de 10 nF, ou de 500 Hz avec des résistances de 10 KO et des condensateurs de 33 nF.
Gain dans la bande passante
Le gain dans la portion de bande passante est ici unitaire (0 dB, pas d'atténuation ni d'amplification) car les résistances R1, R2 et R3 ont des valeurs identiques. Si vous voulez que le filtre apporte une atténuation ou une amplification, il faut alors appliquer un coefficient aux deux résistances R2 et R3, selon les formules suivantes :R2 = R1 * Gain
R3 = R1 / Gain
Rappelez-vous bien cependant que la modification de la valeur des résistances R2 et R3 influence aussi sur la valeur de la fréquence de coupure...
Exemple 1 - Gain de -6 dB (atténuation dans un rapport de 2)
R1 = 10 K0
R2 = R1 * 0.5 = 5 KO
R3 = R1 / 0.5 = 20 KO
Exemple 2 - Gain de +6 dB (amplification dans un rapport de 2)
R1 = 10 K0
R2 = R1 * 2 = 20 KO
R3 = R1 / 2 = 5 KO
Facteur de qualité
Le facteur de qualité Q du filtre (appelé aussi coefficient de surtension) dépend du rapport de valeurs entre C2 et C1, et répond à la formule suivante :Q = (1 / 3) * racine(C1 / C2)
Un coefficient de surtension élevé impose des valeurs très différentes pour C1 et C2. Par exemple, un facteur Q de 50 correspond à un rapport de 22500 entre les valeurs de C1 et C2 (C1 ayant la valeur la plus élevée). En pratique, ce genre de filtre n'est pas très bien adapté pour une valeur élevée du facteur Q.
Remarques
- L'entrée non-inverseuse de l'AOP est reliée directement à la masse, ce qui peut avec certains types d'AOP occasionner une petite tension continue de décallage en sortie. Si tel est le cas et si cela pose un problème, insérer une résistance entre l'entrée non-inverseuse et la masse, de valeur identique à celle de R2. Cette résistance additionnelle n'intervient pas dans la fonction de transfert du filtre, dont la fréquence de coupure reste inchangée.Le schéma du filtre 008b - Passe-haut
Avant d'attaquer le filtre passe-haut actif 008b, un petit rappel
concernant le filtre passe-haut passif... (vous deviez vous en douter
un peu).Filtre passe-haut passif
Le filtre passe-haut le plus simple que l'on puisse concevoir est de type passif et comporte seulement deux composants : une résistance et un condensateur. Par rapport au schéma du filtre passe-bas passif, les deux composants R et C ont été intervertis.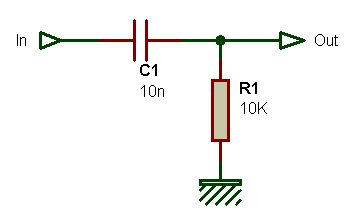
La réponse en fréquence de ce filtre de type "premier ordre" est semblable à la courbe suivante, la pente d'atténuation est de 6 dB par octave (amplitude électrique 2 fois moindre à chaque fois que l'on divise la fréquence par deux) à partir de la fréquence de coupure, qui dépend toujours de la valeur donnée aux deux composants R et C.
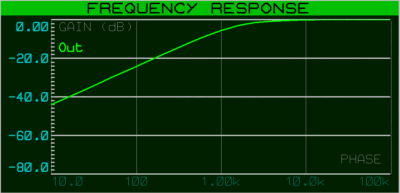
La pulsation w0 du filtre est définie par la formule suivante :
w0 = 1 / (R1 * C1)
La fréquence de coupure Fc (à -3 dB) quant à elle est définie par la formule suivante :
Fc = 1 / (2 * Pi * R1 * C1)
Ici, nous avons, avec R1 = 10 KO et C1 = 10 nF :
w0 = 1 / (10000 * 0,00000001) = 10000
Fc = 1 / (2 * Pi * 10000 * 0,00000001) = 1,59 KHz
Filtre passe-haut actif (008b)
Le filtre actif proposé à la suite est fort similaire au
fltre actif passe-bas vu précédement. Il s'agit là
encore d'un filtre à contre-réaction
multiple adoptant la
structure de Rauch.
Sans grande surprise, la courbe amplitude / fréquence de ce filtre présente la même pente de 12 dB par octave (amplitude électrique 4 fois moindre à chaque fois que l'on divise la fréquence par deux) à partir de la fréquence de coupure :
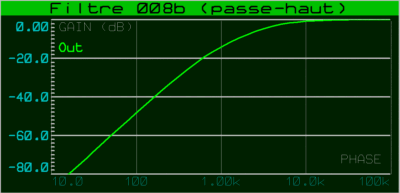
Fréquence de coupure
La fréquence de coupure dépend encore une fois directement de la valeur donnée aux composants R et C. Si les trois condensateurs ont même valeur (C) et si les deux résistances ont aussi même valeur (R), la pulsation w0 du filtre peut alors être représentée par une formule on ne peut plus simple, qui est identique à celle vue avec le filtre passe-bas passif précédent :w0 = 1 / (R * C)
Ce qui donne là encore pour la fréquence de coupure :
Fc = 1 / (2 * Pi * R * C)
Avec les valeurs du schéma, nous avons :
w0 = 1 / (10000 * 0,00000001) = 10000
Fc = 1 / (2 * Pi * 10000 * 0,00000001) = 1,59 KHz
Comme nous avons affaire à une fonction "linéaire", le fait de doubler la valeur des résistances ou des condensateurs a pour effet de baisser la fréquence de coupure dans un même rapport de deux. Si la fréquence de coupure est de 1,59 KHz avec des résistances de 10 KO et des condensateurs de 10 nF, alors elle sera de 15,9 KHz avec des résistances de 10 KO et des condensateurs de 1 nF, ou de 159 Hz avec des résistances de 100 KO et des condensateurs de 10 nF.
Le schéma du filtre 008c - Passe-bande
Devinez quoi... Filtre passe-bande passif
Le filtre passe-bande le plus simple que l'on puisse concevoir est de type passif et comporte quatre composants, il s'agit en fait d'une simple mise en série d'un filtre passe-bas passif avec un filtre passe-haut passif.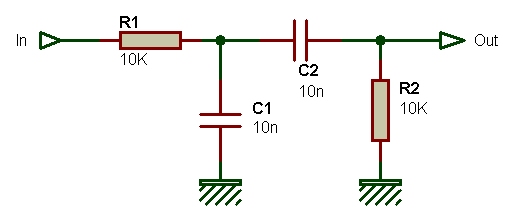
Et chose peu surprenante quand on y réfléchi un peu, la courbe amplitude / fréquence est un "mélange" des deux filtres passe-bas et passe-haut.
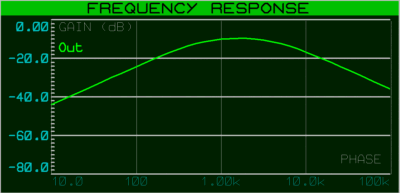
Et devinez voir un peu la valeur de la fréquence centrale ? Gagné ! La fréquence centrale de ce filtre passe-bande est égale à la fréquence de coupure Fc (à -3 dB) des deux filtres passe-bas et passe-haut mis en série, à condition bien sûr que R1 = R2 = R et que C1 = C2 = C.
Fc = 1 / (2 * Pi * R * C)
Ici, nous avons, avec R1 = R2 = 10 KO et C1 = C2 = 10 nF :
Fc = 1 / (2 * Pi * 10000 * 0,00000001) = 1,59 KHz
Filtre passe-bande actif (008c)
Et oui, rien ne se crée, rien ne se perd, tout se transforme.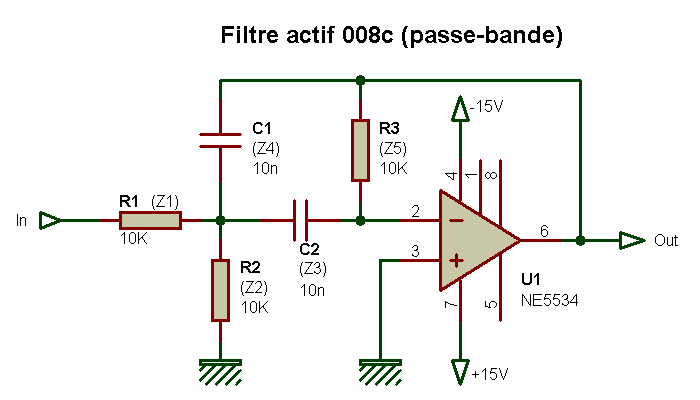
Mêmes pentes de 12 dB par octave de part et d'autre de la fréquence centrale.
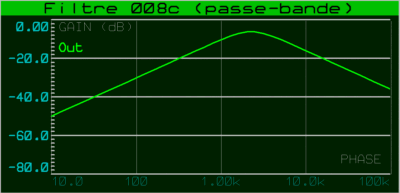
Calcul de la fréquence centrale grâce à la formule suivante, sachant que C1 = C2 = C :
Fc = (1 / (2 * Pi * C)) * Racine((R1 + R2) / (R1 * R2 * R3))
Si R1 = R2 = R3 = R, la formule peut être simplifiée ainsi :
Fc = (1 / (2 * Pi * C)) * Racine((2 * R) / (R^3))
Ici, nous avons, avec R = 10 KO et C = 10 nF :
Fc = (1 / (6.28 * 0.00000001)) * Racine(20000 / (1 * 10^12))
Fc = 15923566 * 0.000141421
Fc = 2252 Hz
Exemple d'application : filtres pour égaliseurs ou pour analyseurs de spectre audio, voir par exemple en page Filtre BF 009.