
Electronique
> Réalisations
>
Diviseur fréquence 004
Dernière mise à jour : 14/07/2014Présentation
Ce diviseur de fréquence possède un facteur de division ajustable entre 1 et 65535, par le biais de microswitches et de compteurs binaires de type CD4040. Il a servi de base à mon générateur d'impulsion 004.Schéma
Le schéma du diviseur se présente ainsi.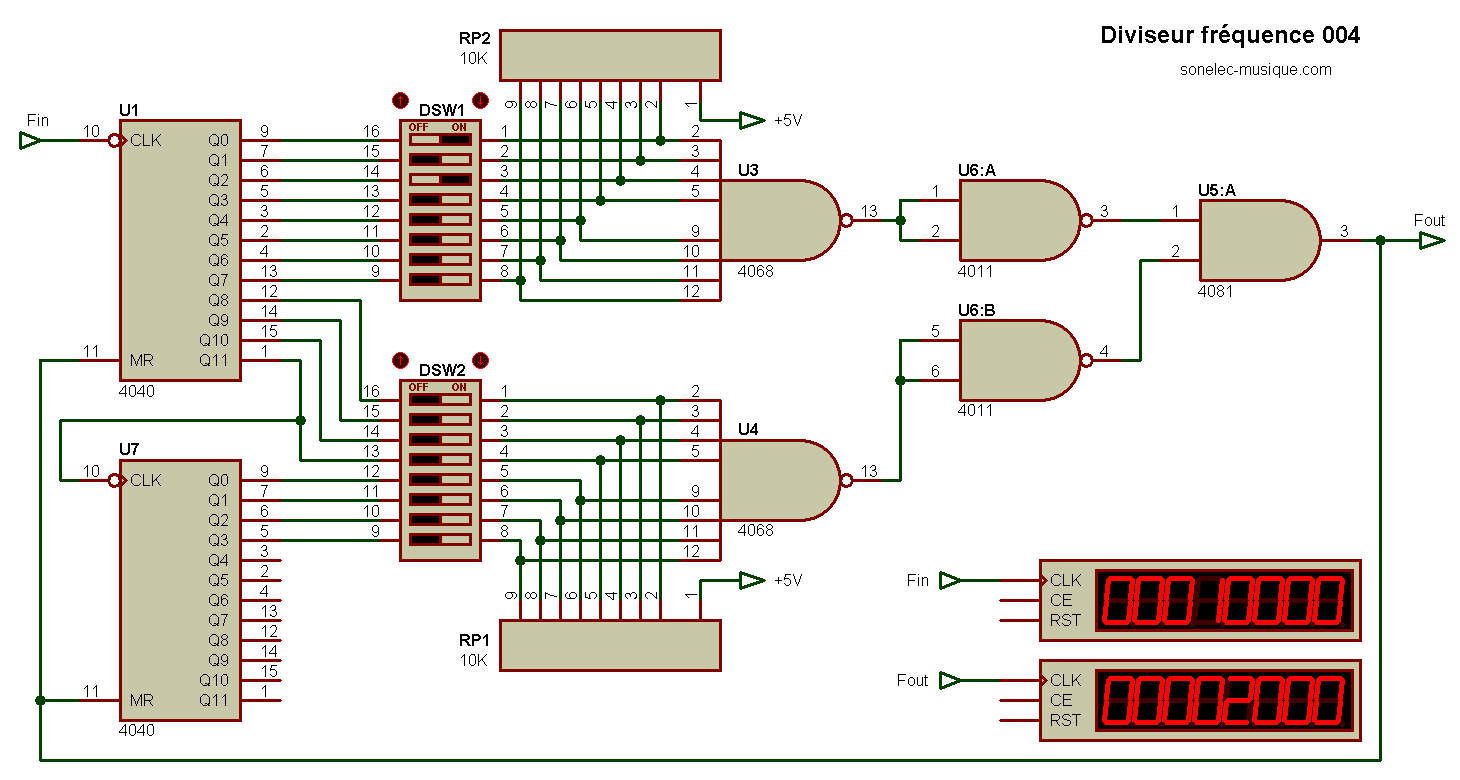
Principe général
L'idée de base est de procéder à un comptage d'impulsions en partant de zéro et en allant jusqu'à une valeur comprise entre 1 et 65535 et choisie par l'utilisateur. Une fois la valeur choisie atteinte, le compteur est remis à zéro et repart pour un tours. Les impulsions de remises à zéro corresponde alors au signal de sortie, dont la fréquence est égale à la fréquence du signal d'entrée divisée par la valeur spécifiée.Comptage
Le comptage doit pouvoir aller jusqu'à 65535, ce qui impose une largeur binaire de 16 bits. Comme je n'ai pas trouvé de compteur binaire possédant de base 16 bits de sorties, je me suis rabattu sur deux compteurs de type CD4040 mis en cascade, la dernière sortie du premier compteur (Q11) aboutissant sur l'entrée horloge du second. Ici, pas d'utilisation possible de CD4020 ou CD4060, auxquels il manque quelques sorties intermédiaires. Ces deux compteurs permettraient d'aller jusqu'à 24 bits mais il ne faut tout de même pas trop exagérer...Si vous souhaitez réduire le comptage (et donc le facteur de division) à la valeur maximale de 255, un bus de 8 bits suffit et vous pouvez alors vous contenter d'un seul compteur CD4040, d'une seule porte AND à 8 entrées et d'un seul ensemble de 8 microswitches.
Détection fin de comptage avec porte AND musclée
Le
but consiste à détecter quand le nombre diviseur que l'on a spécifié
est atteint. Par exemple, si on programme le nombre 5, il nous faut une
information qui revienne toutes les 5 impulsions d'horloge (signal
d'entrée à diviser). Cette information doit en même temps remettre à
zéro les compteurs. La solution la plus logique consiste à employer une
porte AND dont le nombre d'entrées est au moins égale au nombre de bits
qui sont actifs (à l'état logique haut) pour le nombre choisi. Pour le
nombre 1, un seul bit est nécessaire, alors que pour le nombre 7, trois
bits sont nécessaires. Comme le nombre de bits activés dépend du nombre
diviseur choisi et qu'il peut varier entre 1 bit (division par 1) et 16
bits (division par 65535), il nous faut une porte AND dont le nombre
d'entrées est variable, ce qui n'existe pas. En revanche, on peut
prendre une porte AND à 16 entrées et n'en utiliser que certaines,
celles qui ne sont pas utilisées étant alors forcées à l'état logique
haut. A priori rien de bien compliqué, si ce n'est que l'on
travaille sur une largeur de "bus" de 16 bits et qu'il n'existe pas (à
ma connaissance tout du moins) de porte AND possédant autant d'entrées.
Il nous faut donc créer cette porte AND avec plusieurs portes logiques
"plus petites" ou avec des diodes (paragraphe suivant). J'ai choisi au
départ d'utiliser deux portes NAND à 8
entrées, suivies de portes à deux entrées destinées à former un tout
comparable à une unique grosse porte AND à 16 entrées. Notez bien que
j'ai employé les deux termes AND et NAND, il n'y a pas d'erreur dans le
texte... Détection fin de comptage avec diodes
Pour la version à diodes, bien plus simple, voici le schéma :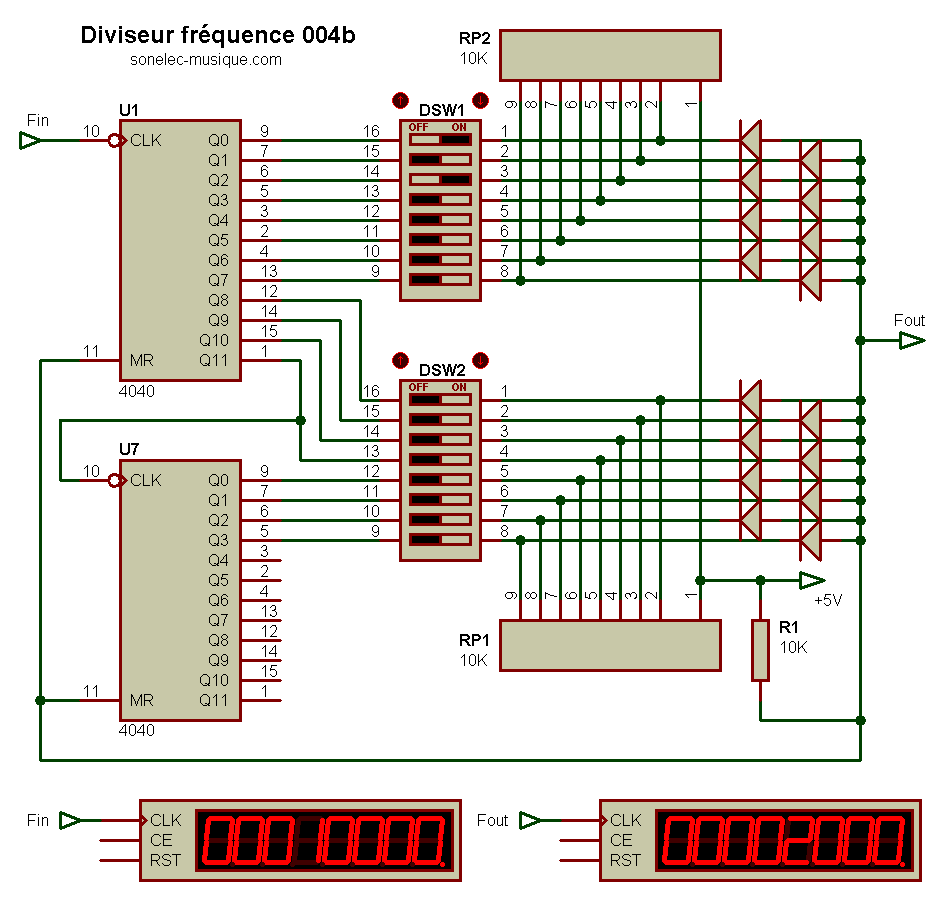
Merci à Xavier qui a pris le temps de m'écrire pour me faire cette suggestion. A croire que j'ai pris goût à compliquer les choses... et à demander aux autres de réfléchir plus que de besoin ;-)
Nouvelle simplification !
Julien B. me fait très justement remarquer que les résistances de rappel au +V ne sont plus utiles avec ce deuxième schéma, et il a bien raison ! On arrive donc au schéma encore plus simplifié qui suit.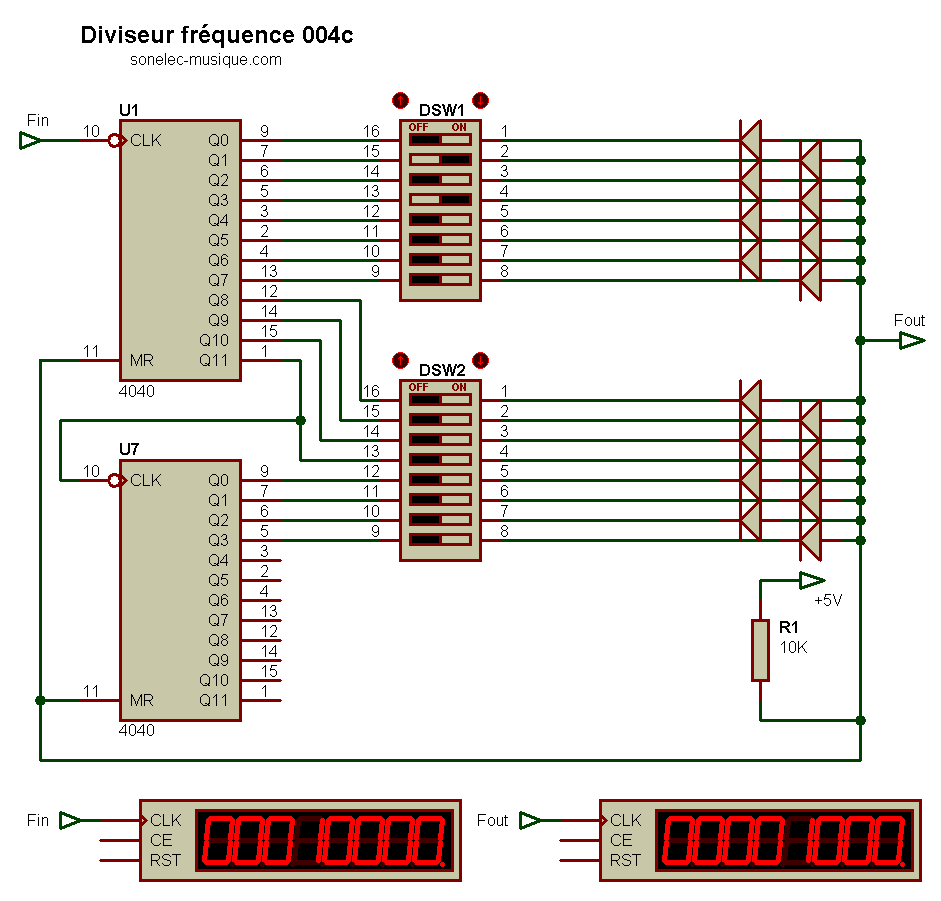
Merci Julien !
Historique
14/07/2014- Ajout schéma 004c, simplifié. Merci à Julien B. pour sa très judicieuse remarque.
29/04/2009
- Première mise à disposition.