
Electronique
> Bases
> Notes de musique
Dernière mise à jour : 05/04/2020Présentation
Le présent article décrit les relations qui peuvent exister entre notes de musique et électronique. Il décrit les relations mathématiques simples qui sont à la base de la génération des notes de musique au moyen d'un appareil électronique, et fournit quelques exemples théoriques de mise en oeuvre pour produire à un instant donné, une note unique (jeu monodique) ou des notes multiples (jeu polyphonique).
Des sonorités différentes
Une note n'est pas perçue de la même façon selon l'instrument qui la produit, vous avez déjà dû vous en rendre compte. En plus de l'aspect lié à la hauteur même de la note, on peut dire que sa perception par nos oreilles et notre cerveau est liée à plusieurs paramètres distincts. Si tel n'était pas le cas, plusieurs instruments différents qui produiraient une note de même hauteur provoqueraient auditivement les mêmes sensations. Les divers paramètres en question ne seront pas abordés ici de façon détaillée car ils peuvent faire l'objet d'un article à part, mais on peut tout de même les lister rapidement :
- Fréquence
- Contenu harmonique
- Enveloppe d'amplitude
- Enveloppe de fréquence
Fréquence
Le son est le fruit d'une variation d'amplitude qui se répète dans le temps, de façon ponctuelle ou permanente. Il peut s'agir d'une variation de pression acoustique autour du point de repos que constitue la pression atmosphérique, ou d'une variation de signal électrique dans un conducteur ou composant électronique (électroacoustique). Le rythme des variations représente (correspond à) la fréquence, c'est le nombre de variations qu'on peut compter dans une période d'une seconde. Si par exemple on mesure 100 variations par seconde, cela signifie que la fréquence est 100 Hz (la période de ce signal est la valeur inverse de la fréquence, soit 1/100 qui équivaut à 0,01 seconde). Plus le nombre de variations par seconde est faible et plus sa fréquence est faible et plus le son est grave, alors qu'une fréquence élevée ou très élevée correspond à un son médium ou aigu (la notion de fréquence faible ou élevée s'applique ici au domaine audio, qui s'étend de 20 Hz à 20 kHz). Chaque note de musique possède une fréquence fondamentale qui lui est propre, certains instruments jouent plutôt dans les graves (basse ou contrebasse par exemple), d'autres se situent plutôt dans le milieu et haut du spectre (piccolo, par exemple). Dans la vraie vie, un instrument ne délivre jamais un son pur uniquement constitué d'une fréquence fondamentale. A cette fréquence "de base" (fondamentale) s'ajoute une ou plusieurs harmoniques. Une harmonique est simplement une fréquence multiple de la fréquence fondamentale. Par exemple, une note de musique peut être constituée d'une fréquence fondamentale de 220 Hz (La2) et de deux harmoniques à 440 Hz (harmonique paire de rang H2) et 660 Hz (harmonique impaire H3). Ce sont les harmoniques (paires ou impaires) qui donnent le timbre et permettre de distinguer des instruments différent qui jouent la même note (à la même fréquence fondamentale).
Contenu harmonique
Selon le nombre et l'amplitude des signaux harmoniques ajoutés à la fréquence fondamentale, une quantité impressionnante de sonorités différentes peut être obtenue. Par exemple, une flute contient un signal de fréquence fondamentale d'amplitude élevé et un contenu harmonique assez faible (le son de la flute est réputé pour être assez "pûr"). En comparaison, le son d'un clavecin, d'un violon ou d'une cymbale est très riche en harmoniques, ce qui rend le timbre de ces instruments très reconnaissable.
Remarques
- Certains instruments produisent des harmoniques dont la fréquence va au-delà du domaine audible (limite supérieure de 20 kHz). Ces harmoniques inaudibles peuvent pourtant provoquer des distorsions gênantes dans le son audible, quand on les numérise avec un appareil dont les paramètres et caractéristiques techniques ne sont pas adaptés (repliement de spectre, entre autres).
- Retirer par filtrage la fréquence fondamentale et ne conserver que les fréquences harmoniques n'empêche pas le cerveau de repérer la hauteur de la note. Il en va de même si on conserve la fréquence fondamentale et qu'on filtre entièrement ou partiellement les harmoniques. Pensez au téléphone qui ne laisse passer qu'une bande de fréquences globalement limitée à la plage 300 Hz à 4 kHz...
Enveloppe d'amplitude
L'amplitude (le volume sonore) d'une note jouée avec une flute à bec reste à peu près constante dans le temps, cet instrument ne permet pas facilement de modifier ce paramètre dans de grandes proportions. Si on souffle trop faiblement ou trop fortement, le son produit n'est pas conforme à ce qu'on attend. En comparaison, l'amplitude d'une note jouée avec un piano évolue fortement dans le temps : volume fort au moment où on frappe la touche, et décroissance progressive du son dans les secondes qui suivent (si on laisse la touche enfoncée pour ne pas bloquer la vibration de la corde qui a été frappée par le marteau). De même, on peut frapper doucement ou fort sur une touche, le son obtenu n'est pas de même force. On conçoit aisement, même sans être expert dans la matière, que produire de façon synthétique une note de piano ne demandera pas les mêmes moyens techniques que ceux requis pour produire de façon synthétique une note de flute à bec.
ADSR (Attack Decay Sustain Release, attaque descente maintien relâchement/extinction) - La courbe ADSR spécifie la manière dont l'amplitude d'un son évolue dans le temps. Chaque élement de cette courbe représente une durée.Enveloppe de fréquence
Ce paramètre est sans doute un peu moins facile à mettre en évidence, mais si vous vous appliquez à écouter la façon dont évoluent certaines notes de musique dans le temps, vous devriez comprendre assez vite de quoi il s'agit. Surtout si ces notes sont jouées de façon "collégiales", une par une, pour ne pas laisser à notre cerveau le loisir de se laisser distraire par d'autres parties sonores. Faites donc l'expérience suivante: sur une guitare, pincez doucement une corde et écoutez bien le son produit, pendant tout le temps où il dure. Puis une fois la note terminée, pincez la même corde mais beaucoup plus fort. Le son produit sera bien sûr plus fort, mais là ne s'arrête pas la différence : avez-vous remarqué que le timbre est différent ? La note ne sonne pas de la même façon, car si la note fondamentale ne change pas, le contenu harmonique lui n'est pas le même. Faites de même avec une touche de piano frappée doucement puis fortement : vous entendrez là encore des écarts de tonalité surprenants. En conclusion : le simple fait de jouer sur le volume sonore (simple réglage d'amplitude de la totalité du son) d'un instrument de musique (électronique ou non) n'est pas toujours suffisant pour reproduire un son faible ou fort fidèle à l'original. Une enveloppe de fréquence peut être naturelle (créée de facto par un instrument acoustique) ou synthétisée avec un ou plusieurs filtres électroniques synchronisés sur le début de la note (pour un effet parfaitement reproductible).
Conclusion rapide
Reproduire le timbre d'un instrument de musique existant nécessite la connaissance des phénomènes physiques de base et la façon dont les paramètres de la note évoluent entre son début (attaque) et sa fin (relâchement/extinction). Un instrument de musique électronique doté d'un premier générateur d'enveloppe qui permet de modifier l'amplitude dans le temps et doté d'un second générateur d'enveloppe qui permet grâce à un ou plusieurs filtres de modifier le contenu fréquentiel (contenu harmonique) dans le temps, autorise la production d'une très riche palette de sons différents. Il va cependant de soi que l'ajout de fonctionnalités de ce type augmente la complexité de réalisation de l'instrument. Dans ce qui suit, seule la notion de hauteur de la note sera abordé.
Relation entre note et fréquence
Si on arrive à entendre une note de musique, c'est que ses propriétés (acoustiques / électriques) sont contenues dans des limites que notre oreille est capable de traiter. La première de ces caractéristiques concerne la fréquence. Le terme "fréquence" peut paraître barbare à certains mais il s'agit d'un terme qu'on ne peut pas ignorer si on s'interresse à la production sonore ou à l'enregistrement sonore. Fort heureusement, il est facile de comprendre à quoi il correspond, dès l'instant où l'on sait (et que l'on comprend) qu'une vibration sonore est définie par une succession de pressions et de dépressions de l'air qui parvient à nos tympans. Imaginez que quelqu'un place sa bouche près de votre oreille, qu'il souffle (doucement) pendant une demi-seconde, puis qu'il aspire (tout aussi doucement) pendant une demi-seconde. En répétant ce geste de façon continue, il produit une suite de pressions et depressions de l'air sur le tympan, à une fréquence de 1 Hz (qui correspond à un cycle complet pression + depression). A cette vitesse, aucune perception sonore n'est possible par le cerveau, il faut augmenter la fréquence pour que l'on puisse commencer à entendre quelque chose. Si le "soufleur / aspirateur" était assez rapide et qu'il pouvait souffler et aspirer à raison de 220 cycles par seconde (220 hertz), vous entendriez une note assez grâve, correspondant à un La2. A une fréquence de 225 Hz, vous entendriez un La2 légèrement désaccordé vers le haut (plus aigu que le La2 "normal"). En réalité, cela est aussi simple que cela : à chaque note de musique correspond une oscillation à une fréquence bien déterminée (oscillation électrique si on regarde dans le domaine électronique, oscillation acoustique si on se place dans l'air). La "forme" même de l'oscillation importe peu : que le "soufleur / aspirateur" passe brutalement du soufflage à l'aspiration (forme plutôt "carrée") ou qu'il procède de façon progressive (forme plutôt "sinusoïdale" ou "triangulaire") ne modifie en rien la fréquence, cela ne joue que sur le timbre et en particulier sur le contenu harmonique. La note est la même mais n'est pas perçue de la même façon, c'est ce qui se passe quand on écoute des notes de même hauteur jouées par un piano, une flute et un violon. La fréquence d'oscillation est un paramètre qui donne à une note son caractère personnel puisque d'elle dépend directement sa hauteur, mais d'autres paramètres importants entrent en ligne de compte dans la perception auditive. C'est ce qui a été entrevu dans le paragraphe précédent.
Relation mathématique entre deux notes de musiques adjacentes
D'un point de vue purement mathématique, la répartition des notes de musique de nos contrées répond à une certaine régularité : il existe un écart identique entre chaque note de musique, égal à "racine douzième de deux".
Ecart entre deux notes = 12 / [racine de 2] = 1,0595
Cela signifie que l'on a le même écart quand on passe de Do3 à Do3#, ou quand on passe de Fa4 à Sol4. Cette régularité n'est pas vrai pour toutes les musiques : c'est la raison pour laquelle par exemple, certaines musiques orientales paraissent sonner "faux" à certains moment, certaines notes de la gamme ne coincidant pas avec celles que nous avons l'habitude d'entendre (avez-vous déjà écouté le son d'un fifre dans une fanfare ?). Sachant que l'écart entre deux notes adjacentes est fixe, on peut en déduire que l'on peut obtenir toutes les notes d'une octave donnéeà partir d'une seule et unique note. D'un point de vue pratique, un instrument de musique électronique dont les notes sont produites de façon individuelle (12 oscillateurs pour une octave complète) est bien plus "instable" et casse-pied à régler, qu'un instrument de musique électronique dont toutes les notes sont produites à partir d'un unique oscillateur. Ce point pratique sera traité dans les lignes qui suivent.
Relation mathématique entre deux notes de musiques espacées de 1 octave
D'un point de vue toujours purement mathématique, l'écart qui existe entre deux notes de même nom sur un intervale de un octave, est plutôt simple, puisqu'il correspond au rapport 2.
Ecart entre deux octaves (même note, par exemple La3 et La4) = 2
La note La3 possède une fréquence d'oscillation fondamentale qui est exactement le double de celle du La2, tout en ayant à la fois une fréquence d'oscillation fondamentale qui est exactement la moitié de celle du La4.
- La2 = 220 Hz (fréquence moitié du La3)- La3 = 440 Hz
- La4 = 880 Hz (fréquence double du La3).
Cet état de fait simplifie considerablement les choses en électronique, puisqu'un diviseur de fréquence par deux est très simple à réaliser. En réalité, un seul circuit intégré logique de type compteur binaire à huit sorties permet d'obtenir toutes les notes identiques (tous les Sol par exemple) de l'octave N° 8 à l'octave N°1 : il suffit de produire la note Sol 8 avec un signal à la fréquence adéquate, que l'on divise ensuite successivement par deux pour obtenir les notes Sol des octaves inférieures. Ainsi, l'ajout d'un compteur binaire à 8 sorties sur chacune des 12 notes de base permet de couvrir la totalité de huit octaves. Répétons que l'on parle ici de la fréquence "de base" des notes : des oscillateurs suivis de diviseurs de fréquence ne permettent d'obtenir que des signaux carrés d'amplitude constante, et il faut ajouter à celà une certaines quantité de composants électroniques si on souhaite générer des formes d'ondes plus variées (un signal rectangulaire n'est pas désagréable à entendre mais on s'en lasse vite).
Tableau récapitulatif de la relation entre note et fréquence
Chaque
note de musique "vibre" à une fréquence bien particulière, le tableau
qui suit montre la relation qui existe entre la valeur d'une note et sa
fréquence (les valeurs hautes ont été arrondies au hertz). Toutes les
valeurs sont exprimées en Hertz, et les notes dont la fréquence est
inférieure à 20 Hz ou supérieure à 20 KHz sont volontairement ignorées
puisque inaudibles par la majorité des auditeurs.| Note | Ecart |
Oct -1 |
Oct 0 | Oct 1 | Oct 2 | Oct 3 | Oct 4 | Oct 5 | Oct 6 | Oct 7 | Oct 8 | Oct 9 |
| Do |
1 (réf.) |
- |
32.703 | 65.406 | 130.81 | 261.63 | 523.25 | 1046.5 | 2093.0 | 4186.0 | 8372.0 | 16704 |
| Do# |
- |
34.648 |
69.296 | 138.59 | 277.18 | 554.37 | 1108.7 |
2217.5 |
4434.9 |
8869.8 |
17739 |
|
| Ré |
1 + 1/8 | - |
36.708 |
73.416 | 146.83 | 293.66 | 587.33 | 1174.7 |
2349.3 |
4698.6 |
9397.3 |
18795 |
| Ré# | - |
38.891 |
77.782 | 155.56 | 311.13 | 622.25 | 1244.5 |
2489.0 |
4978.0 |
9956.1 |
19912 |
|
| Mi |
1 + 2/8 | 20.602 |
41.204 |
82.407 | 164.81 | 329.63 | 659.26 | 1318.5 |
2637.0 |
5274.0 |
10548 |
- |
| Fa |
1 + 1/3 | 21.827 |
43.654 |
87.307 | 174.61 | 349.22 | 698.46 | 1396.9 |
2793.8 |
5587.7 |
11175 |
- |
| Fa# | 23.125 |
46.249 |
92.499 | 185.00 | 369.99 | 739.99 | 1480.0 |
2960.0 |
5919.9 |
11840 |
- |
|
| Sol |
1 + 4/8 | 24.500 |
48.999 |
97.999 | 196.00 | 392.00 | 783.99 | 1568.0 |
3136.0 |
6271.9 |
12544 |
- |
| Sol# | 25.957 |
51.913 |
103.83 | 207.65 | 415.30 | 830.61 | 1661.2 |
3322.4 |
6644.9 |
13290 |
- |
|
| La |
1 + 2/3 | 27.500 |
55.000 | 110.00 | 220.00 | 440.00 | 880.00 | 1760.0 | 3520.0 | 7040.0 | 14080 | - |
| La# | 29.135 |
58.270 |
116.54 | 233.08 | 466.16 | 932.33 | 1864.7 |
3729.3 |
7458.6 |
14917 |
- |
|
| Si |
1 + 7/8 | 30.868 |
61.735 |
123.47 | 246.94 | 493.88 | 987.77 | 1975.5 |
3951.1 |
7902.1 |
15804 |
- |
Formule pour relation entre note et fréquence
Freq = 16.3516 * 2 ^ ((Oct + 1) + ((NoteRank - 1) / 12))Freq étant la fréquence exprimée en Hertz, Oct étant l'octave (de 1 à 9) et NoteRank étant le rang de la note
- NoteRank = 1 pour Do- NoteRank = 2 pour Do#
- ...
- NoteRank = 11 pour La#
- NoteRank = 12 pour Si
Exemple pour la note La3 :
Freq = 16.3516 * 2 ^ ((3 + 1) + ((10 - 1) / 12))Freq = 16.3516 * 2 ^ (4 + (9 / 12))
Freq = 16.3516 * 2 ^ (4,75)
Freq = 440,000 Hz
Comment obtenir les 12 notes à partir d'une seule fréquence ?
Chacune des 12 notes d'une octave peut être obtenue en divisant un même signal de fréquence fixe par différents taux de division qui sont les suivants :
| Note | Taux de division |
| Si | 239 |
| La# | 253 |
| La | 268 |
| Sol# | 284 |
| Sol | 301 |
| Fa# | 319 |
| Fa | 338 |
| Mi | 358 |
| Ré# | 379 |
| Ré | 402 |
| Do# | 426 |
| Do | 451 |
Ainsi, pour produire un LA4 de 880 Hz, il faut un oscillateur délivrant un signal de fréquence 235,84 kHz (880 Hz * 268).
Comment produire une note de musique ?
Produire une note de musique avec des moyens électroniques est vraiment très simple, vous pouvez me faire confiance. Produire plusieurs notes qui soient bien stables dans le temps est un peu moins simple mais loin d'être insurmontable. La première décision à prendre, quand on veut réaliser un instrument de musique électronique avec des notes activées par des touches (classiques ou sensitives) concerne le nombre de notes que l'on veut pouvoir jouer simultanement. Fabriquer un orgue monodique qui n'autorique qu'une seule note à la fois est très simple, bien plus simple que de fabriquer un orgue polyphonique qui autorise la production de plusieurs notes en même temps. Dans ce qui suit, il ne sera abordé que l'aspect production des fréquences de base, l'aspect mise en forme est volontairement ignoré car faisant partie d'un vaste sujet qui mérite un livre entier à lui tout seul.
Produire une seule note à la fois
L'exemple pratique qui suit met en oeuvre un oscillateur simple, qui génère un signal de fréquence fixe et voisine de 440 Hz.
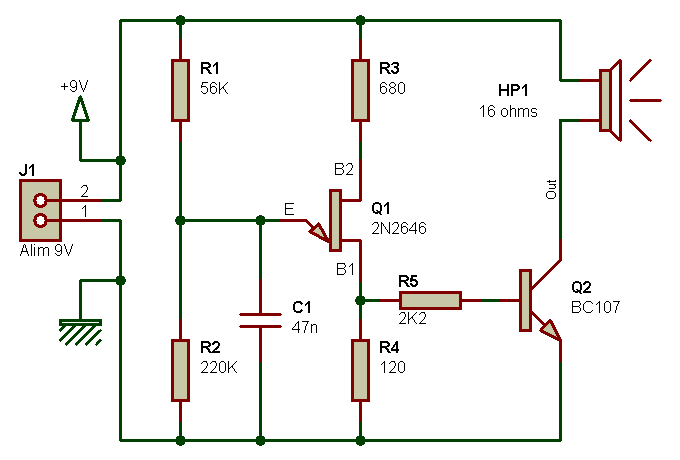
Du fait de l'absence de réglage, et du fait que les composants électroniques qui déterminent la fréquence d'oscillation possèdent une valeur inconnue au moment de l'achat (à cause de leur tolérance), il est absolument impossible de prédire si le son généré correspondra oui ou non à une note existante. Pour pouvoir "accorder" l'oscillateur sur une note existante, il convient de rendre variable un des élements qui ont une influence sur la fréquence d'oscillation, ici R1 et C1. On pourrait ainsi remplacer le condensateur C1 par un modèle variable, mais se pose un problème de taille : les condensateurs ajustables sont plus faciles à trouver et sont moins volumineux quand il s'agit de faibles valeurs capacitives (quelques pF ou dizaines de pF). Dans le cas présent, ce n'est pas une solution que l'on peut retenir. Le remplacement de la résistance R1 par un potentiomètre ajustable pose bien moins de problèmes : les résistances ajustables existent sur de larges plages de valeurs et elles ne prennent pas trop de place... tout du moins tant qu'on envisage pas la fabrication d'un instrument fonctionnant sur six octaves ! Le schéma suivant permet donc de produire une note dont on peut régler avec précision la hauteur tonale, grâce au potentiomètre RV1.
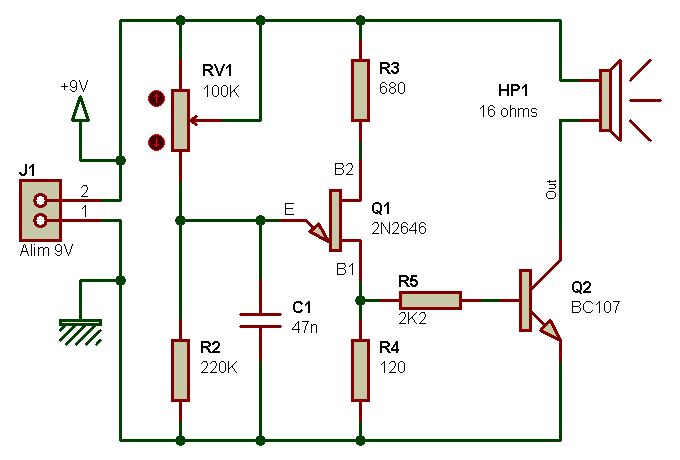
Si maintenant on remplace RV1 par un ensemble de plusieurs potentiomètres ajustables dont un seul est mis en service à la fois (avec un bouton poussoir ou avec une pointe de touche que l'on promène sur des punaises), et où chaque potentiomètre est réglé pour obtenir une note donnée, on obtient un mini-orgue fort simple et qui fonctionne du premier coup :
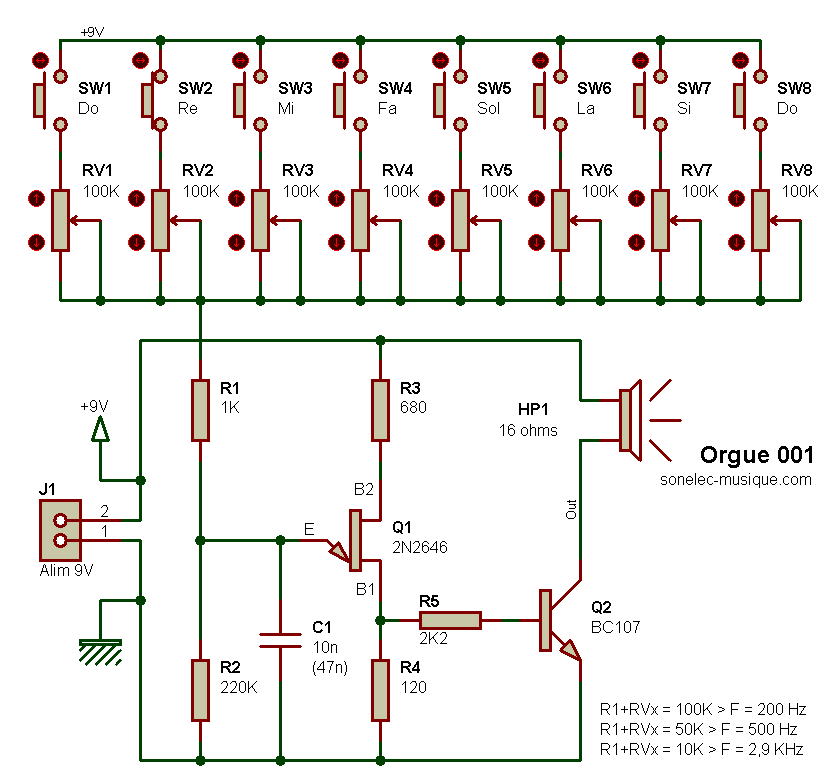
Détails de ce circuit à la page Orgue 001
Mais cette simplicité se paie, et un point noir vient salir ce beau tableau de la simplicité : une stabilité en fréquence bien trop dépendante de la température environnante. Tous les composants mis en oeuvre ici contribuent plus ou moins à la stabilité de la fréquence du signal généré, et même le potentiomètre ajustable peut être couplable de fortes dérive (un modèle Cermet est plus stable mais aussi plus cher). Ce type de montage se prête bien à l'expérimentation, mais ne convient plus pour un instrument sérieux qui ne nécessite pas dix reprises de réglage au cours d'un même concert. Mais alors, comment obtenir une fréquence stable ? Je le lis sur vos lèvre, le mot vous brûle dans la bouche : un oscillateur à quartz, bien sûr ! Très bien, partons donc sur ce principe. Un oscillateur à quartz, qui vibre directement à la fréquence de la note désirée, comme devrait le permettre le schéma suivant.
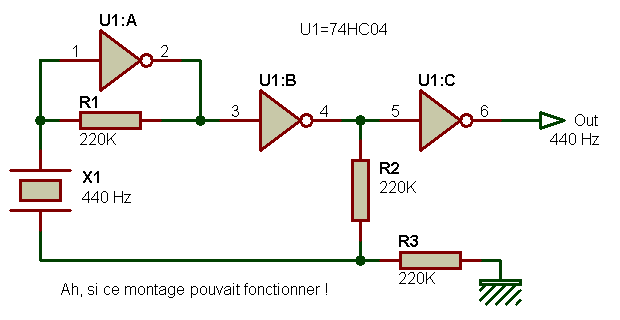
Hum, le quartz idoine de 440 Hz n'est pas facile à trouver, n'est-ce pas ? Qu'à cela ne tienne : on en prend un de valeur élevée que l'on trouve facilement (par exemple 1 MHz) et on procède à une division de fréquence qui permet d'obtenir un signal final qui correspond au besoin. Pour simplifier le circuit diviseur, on peut remplacer les compteurs et portes classiques par un composant programmable qui fait ce qu'on lui demande.
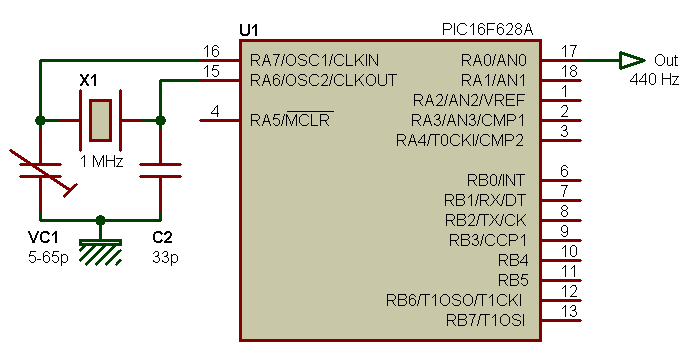
Le matheux aura vite fait de faire remarquer que 1 MHz divisé par 440 ne donne pas une valeur entière, et qu'il est donc impossible d'obtenir du 440 Hz pile avec une horloge de base à 1 MHz. Ceci est juste, et on peut répondre qu'il n'y a qu'à ajuster un peu la fréquence d'oscillation à l'aide du condensateur ajustable VC1, afin de "dérégler" légèrement l'horloge 1 MHz et ainsi de s'approcher au plus près du 440 Hz attendu. Méthode qui se tient en théorie. Mais vous voyez le tableau si on veut générer les 12 notes d'une octave ? Beaucoup de composants programmables et de quartz, et beaucoup de dépenses pour un résultat somme toute assez limité. Il faut donc trouver une autre solution. Conserver un seul oscillateur suivi d'un diviseur de fréquence dont le taux de division dépend de la touche enfoncée ? Oui, cela est envisageable et pourrait être mis en oeuvre. Ce serait encore un peu compliqué sans composant programmable, mais pas impossible. En fait, dès qu'on essaye de produire des notes de façon stable avec un oscillateur à quartz et des diviseurs de fréquence, on se rend compte que cela devient aussi compliqué que de vouloir créer un instrument pouvant jouer plusieurs notes à la fois. Alors, quitte à compliquer les choses, autant tirer d'autres profits que la seule stabilité en fréquence.
Produire plusieurs notes à la fois
Le petit instrument de musique électronique réalisé avec quelques composants de récupération et appelé Orgue 001 est fort sympathique, mais voilà 20 ans que vous l'avez réalisé et il est maintenant temps de passer à l'étape supérieure. Le magasin du coin propose en ce moment une supère affaire : un orgue électronique 49 touches, avec 1000 sons différents, des rythmiques et des accompagements intégrés. Le tout pour 100 euros. Cela vaut-il donc le coup (le coût) de faire soi-même sa machine ? La réponse est bien sûr non si on s'en tient au seul aspect financier. Vous n'arriverez probablement pas à faire autant avec la même dépense, en supposant même que vous trouviez tous les composants nécessaires. L'intérêt réside bien entendu dans l'apprentissage, les essais, les modifications et surtout dans le côté modulaire du système : vous pouvez très bien pour commencer prévoir un module de base et y ajouter ensuite des modules annexes pour augmenter les capacités sonores de l'instrument. Le but de ce paragraphe n'est donc que de donner un aperçu sur la façon de partir sur une base utile, qui pourrait fort bien suffire pour de petits besoins. A la base donc, une seule fréquence : un oscillateur unique, à partir duquel on peut produire toutes les autres notes, est une solution élégante et heureusement facile à mettre en oeuvre avec les composants actuels. Je dois tout de même avouer qu'il fut une époque où je regardais tout ça d'un autre oeil : les schémas disponibles mettant en oeuvre des composants spécialisés tels les xxxwwwzzz, ne pouvaient que faire un peu peur : disponibilité et prix n'étaient pas forcement compatibles avec argent de poche. Aujourd'hui, j'ai compris que l'on pouvait faire simple et peu coûteux, c'est la raison de ces quelques mots. Bien, nous partons donc d'un oscillateur unique, que l'on peut éventuellement prévoir ajustable pour permettre l'accordage avec d'autres instruments. A la suite de cet oscillateur fixe, un ensemble de diviseurs de fréquence fixes permettant de produire chaque note de base, sur une octave donnée.
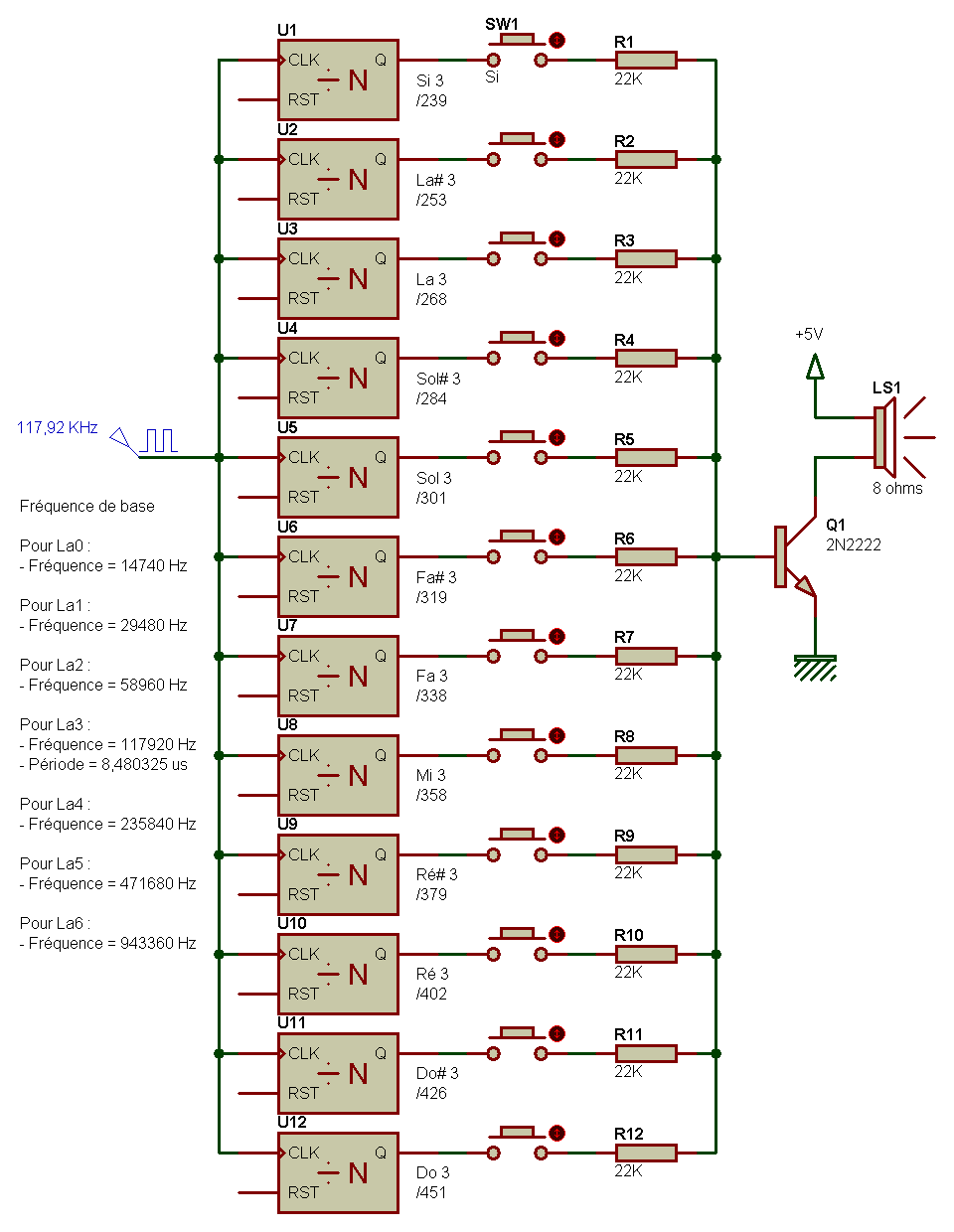
Ensuite, des diviseurs de fréquence par deux pour délivrer les notes des octaves inférieures, comme le montre le schéma quelque peu simplifié qui suit.
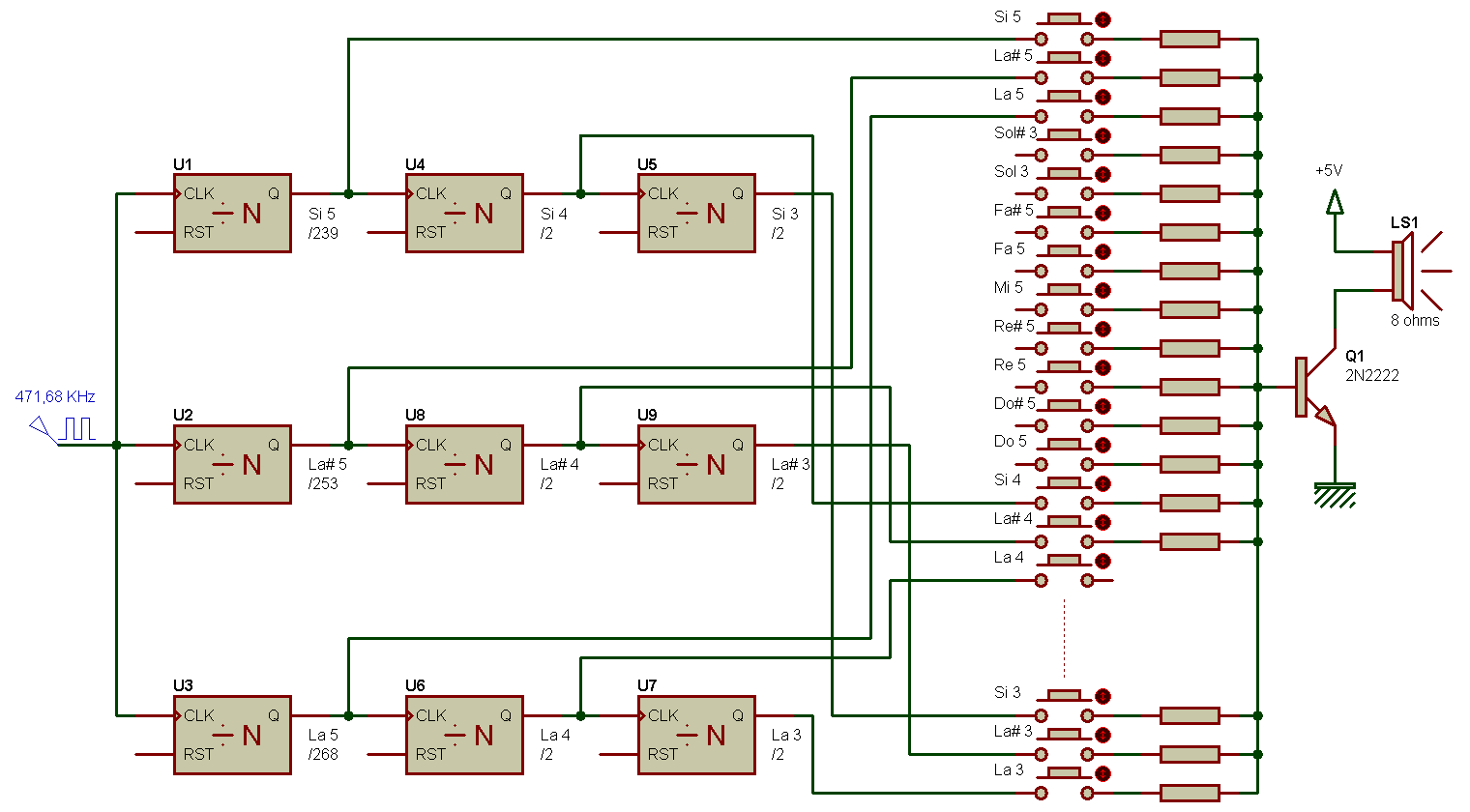
Le schéma qui précède pourrait aussi être présenté de la façon suivante, où plusieurs diviseurs sont inclus dans une même boite, rendant par là-même la lecture du schéma plus facile :
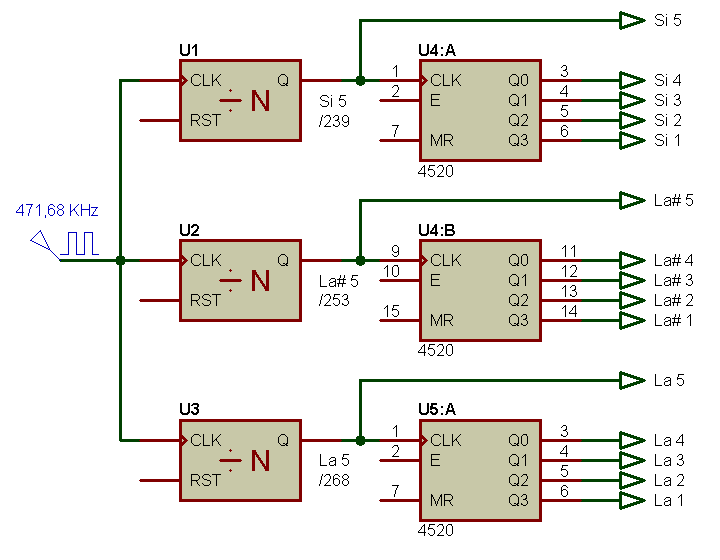
Il n'est certes pas très compliqué de diviser un signal de fréquence donné avec un rapport fixe, il suffit d'un compteur et de quelques portes logiques. Oui, mais pour une note. Ce qui commence à devenir "usine à gaz" pour la totalité des douze notes. Pour faire plus simple, il est peut-être possible d'utiliser un petit composant programmable bon marché de type PIC (Microchip) programmé pour le faire fonctionner en diviseur de fréquence multiple : une entrée pour accueillir le signal d'horloge de référence, et 12 sorties pour produire les 12 notes de base qui attaquent ensuite les diviseurs de fréquence par deux (les compteurs binaires CD4520 dans le cas présent). C'est une voie que j'ai essayé d'explorer (Orgue 003), je n'y suis arrivé que partiellement car la fréquence d'entrée à diviser est trop élevée pour un PIC tel que celui choisi (l'écart entre notes est correct mais les notes produites sont à basse fréquence, ce qui m'empêche de faire suivre le PIC des diviseurs par deux - mais j'ai tout de même entre les mains un petit instrument assez fonctionnel).
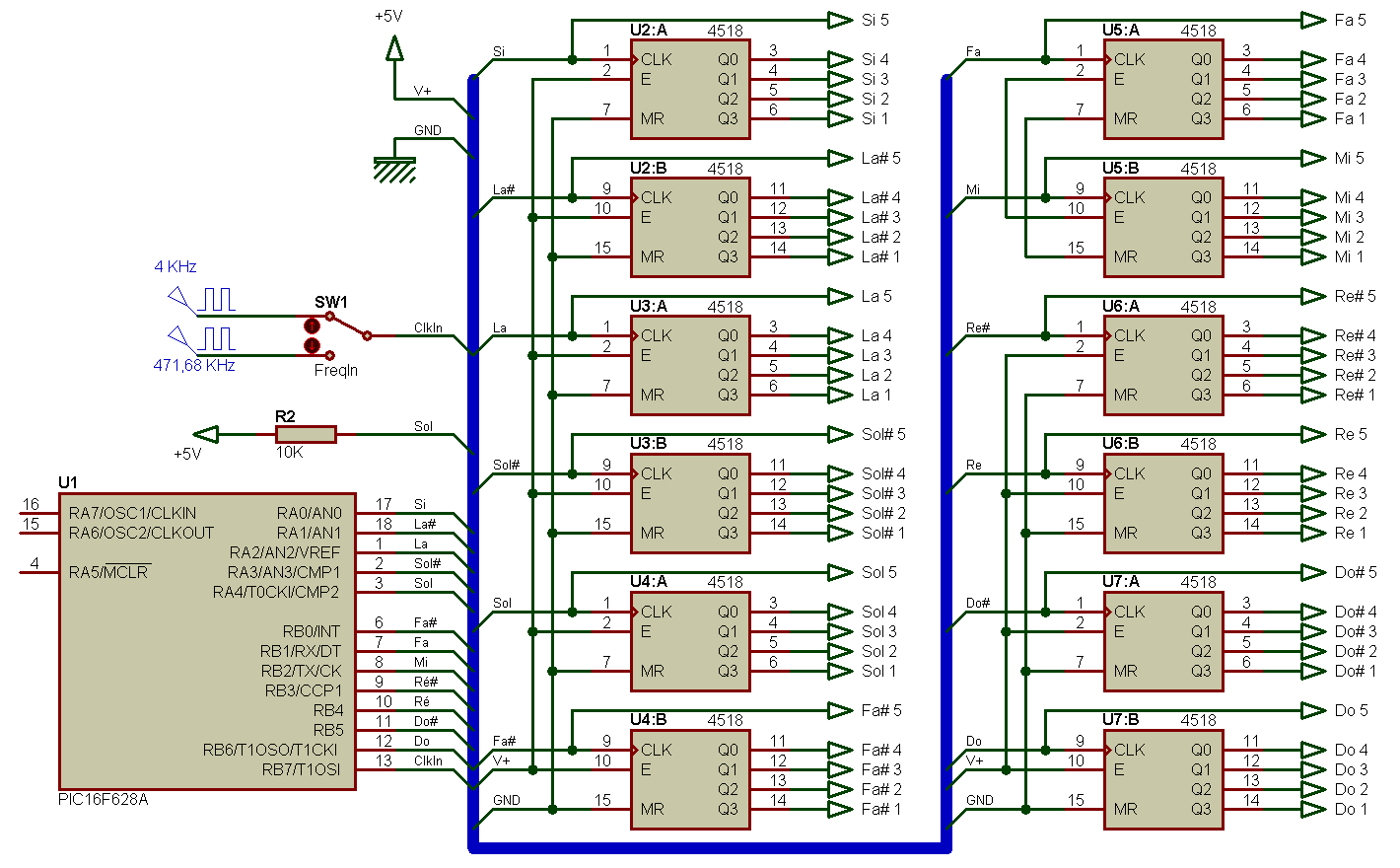
Principe de base de mon orgue 003
Si cela peut fonctionner ainsi, il sera difficile de faire plus simple... rappelez-vous qu'il s'agit d'un instrument polyphonique avec lequel toutes les notes peuvent être jouées en même temps ! Et ce circuit aurait un avantage de taille : toujours la même progression entre chaque note, quelque soit la fréquence du signal d'entrée. Ce qui veut dire que l'on pourrait envisager de choisir une fréquence d'entrée facile à produire (quartz courant ou même simple oscillateur RC ou LC) quitte à ne pas pouvoir s'accorder précisement avec d'autres instrument (non critique pour ceux qui aiment jouer seul).
Quelques circuits anciens
Je n'ai jamais eu l'occasion de travailler avec les circuits d'orgue de l'époque, mais il m'est arrivé de voir quelques schémas de mise en oeuvre. Le seul orgue électronique que j'ai eu entre mes mains (pendant quelques années) fonctionnait bien et je n'ai jamais éprouvé le besoin d'aller plus loin que d'ouvrir l'engin pour voir "en gros" ce qu'il contenait. Il faut dire que j'avais 12 ans, ma maman avait acheté ce volumineux appareil pour une bouchée de pain dans un entrepôt récupérant des articles de magasins en faillite.
Diviseurs à transistors
Avant l'utilisation systématique de circuits intégrés (assez coûteux au début), l'usage de transistors était répendu pour assurer la division des signaux générés par les oscillateurs de base. On peut en effet utiliser un multivibrateur bistable composé de deux transistors classiques, pour diviser un signal d'horloge par deux. Un schéma de ce type est proposé à la page Diviseurs de fréquence.
AY-1-0212 (General Instrument)
Ce circuit intégré produisait l'ensemble des 12 notes de base à partir d'un oscillateur externe unique tournant à 2 MHz. Il était suivi de diviseurs de fréquence tel les SAJ110.
MOST 7D1 (Armel)
Ce circuit intégré de type DIL14 était associé à un oscillateur de base (souvent à base de transistor UJT) et permettait de diviser une fréquence de base par 2, 4, 8, 16, 32, 64 et 128. Avec 12 oscillateurs de base, il permettait donc de travailler sur 8 octaves complets. Il pourrait aujourd'hui être remplacé sans problème par un compteur binaire de type CD4040.
SAA1030 (ITT Semiconducteurs)
Ce circuit intégré produisait l'ensemble des 12 notes de base à partir d'un oscillateur externe unique tournant à 4,68864 MHz. Il pouvait être suivi de diviseurs de fréquence tel les SAJ110.
SAA1900 (ITT Semiconducteurs)
Ce circuit intégré incluait toutes les fonctions de base d'un miniorgue électronique pourvu de 56 touches groupées en deux parties Solo et Accompagnement. Le circuit était cadencé sur une horloge externe de 500 KHz.
SFF5009 (Sescosem)
Ce circuit intégré produisait l'ensemble des 12 notes de base à partir d'un oscillateur externe unique. Il pouvait être suivi de diviseurs de fréquence tel les SAJ110 ou SAJ180 (Sescosem) ou SAH220 (RTC).
MO61 (SGS-Ates)
Ce circuit intégré produisait lui aussi l'ensemble des 12 notes de base à partir d'un oscillateur externe. Pour obtenir les notes les plus hautes (avant division pour obtenir les notes des octaves inférieures) la fréquence de cet oscillateur externe devait être de :
- 58,960 kHz pour un LA2 à 220 Hz (220 Hz * 268)
- 117,92 kHz pour un LA3 à 440 Hz (440 Hz * 268)
- 235,84 kHz pour un LA4 à 880 Hz (880 Hz * 268)
- 471,68 kHz pour un LA5 à 1760 Hz (1760 Hz * 268)
- 943,36 kHz pour un LA6 à 3520 Hz (3520 Hz * 268)
Sans surprise, on retrouve notre rapport de 2 pour la fréquence d'oscillateur pour chaque passage d'une octave à l'autre.
Voir aussi Ces composants qu'on trouvait si pratiques.