Sommaire | Services Pro | Musiques | Publications | Connectique | Electronique | Logiciels | Divers | Contacts | Liens | Glossaire | Historique

Electronique > Bases > Les diviseurs de tension résistifs

Dernière mise à jour : 07/03/2007

Présentation

Un diviseur de tension est un système qui permet de fournir une tension de sortie donnée (par exemple 5V) à partir d'une tension d'entrée donnée (par exemple 7V). La valeur de la tension de sortie est toujours plus faible que celle de la tension d'entrée, ça ne peut pas être autrement avec ce type de système. On parle de diviseur de tension parce que la tension de sortie est une fraction de la tension d'entrée, il existe un rapport simple entre les deux valeurs. Le présent article se réfère aux diviseurs de tension de type résistif. Il existe d'autres types de diviseurs de tension (diviseurs de tension capacitifs par exemple), c'est pourquoi je précise bien "résistifs". Ce type de diviseur de tension est largement utilisé :
- pour permettre à un voltmètre de disposer de plusieurs calibres (0.2V, 2V, 20V, 200V, 2000V, par exemple);
- pour la création d'une masse virtuelle dans un montage analogique audio;
- pour la définition de plusieurs seuils dans un circuit d'affichage ou de mesure, tel qu'un thermomètre ou un vumètre à leds, par exemple.
La suite de l'article suppose que vous connaissiez déjà vos besoins en terme de tensions désirées. Il explique en effet comment calculer la valeur des résistances requises en fonction des tensions disponibles et des tensions divisées (diminuées) souhaitées.
Remarque : vous trouverez sur cette page plusieurs schémas électroniques, où sont notées plusieurs valeurs de tension. Toutes les tensions sont mesurées par rapport à la masse, qui sert de point de référence.

Diviseur de tension simple

Deux résistances suffisent pour constituer un diviseur de tension. La valeur à donner à ces résistances n'est pas forcement simple à déterminer, mais nous verrons cela le moment venu. Commençons donc par le principe de base, en analysant le schéma simple suivant, qui montre la mise en oeuvre d'un diviseur de tension constitué de deux résistances R1 et R2, et où la tension de sortie Vs répond à la formule suivante :
Vs = Ve * (R2 / (R1 + R2))

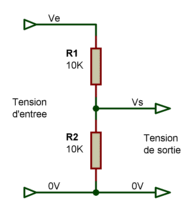Les deux résistances R1 et R2 sont reliées en série, et on applique sur celles-ci, une tension d'entrée Ve, Ve étant la tension dont on dispose et avec laquelle on veut obtenir une autre tension. Si les résistances ont la même valeur ohmique, ce qui est le cas sur ce schéma, elles vont s'approprier chacune la même portion de tension. Puis on "récupère" la tension disponible sur la résistance R2, qui est connectée à la référence 0V. On obtient sur cette résistance une tension de sortie Vs, qui est la tension que l'on désire obtenir à partir de la tension d'entrée Ve. Comme les deux résistances ont ici la même valeur, on récupère en sortie, une tension Vs égale à la moitié de la tension d'entrée Ve.

"Comme les deux résistances ont ici la même valeur, on récupère en sortie, une tension Vs égale à la moitié de la tension d'entrée Ve.". Cela est vrai si l'on considère que tout est parfait, c'est à dire :
- si la source de tension Ve possède une résistance de source (résistance série) nulle;
- si les deux résistances ont effectivement la même valeur;
- si le circuit qui va exploiter la tension de sortie Vs possède une résistance d'entrée (résistance parallèle) infinie.
Comme vous le savez sans doute déjà, le monde parfait n'est pas le notre. Les conditions énnoncées ci-avant ne seront pas respectées. La source de tension possède une résistance interne qui n'est pas nulle, la valeur réelle d'une résistance n'est pas forcement celle qui est indiquée dessus (à cause de sa tolérance), et la tension de sortie sera appliquée à un circuit qui ne possèdera pas une résistance interne infinie. Mais l'important est de savoir si ce qui n'est pas parfait est utilisable ou non. Ou de faire en sorte que cela soit le cas. Prenons un exemple pratique, où l'on veut obtenir une tension de 4.50V à partir d'une tension de 9.00V. Après ce qui a été vu ci-avant, on se dit que deux résistances de 10K chacune font parfaitement l'affaire, et on l'adopte donc. Dans le schéma qui suit, nous reprenons donc le même schéma que celui vu avant, mais afin de bien mettre en évidence les problèmes potentiels, tous les défauts énumérés ci-avant sont volontairement exagérés (mais pas tant que ça). A savoir l'utilisation d'une source de tension Ve qui possède une forte résistance interne RS de 1 Kohms, des résistances réelles R1 et R2 qui ne font pas parfaitement 10 Kohms (ce sont des modèles ayant une tolérance de 5%), et un circuit "utilisateur" qui présente une résistance d'entrée RE de 20 Kohms.



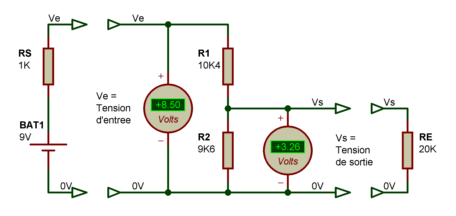
On constate que les 4.50V attendus ne font en fait que 3.26V, ce qui ne va pas du tout ! A quoi cela est-il dû ? Au simple fait que la résistance "parasite" RS est mise en série avec R1, et que la résistance "parasite" RE est mise en parallèle avec R2. C'est comme si on disposait d'un pont diviseur avec une résistance R1 de 11.4 Kohms et une résistance R2 de 6.5 Kohms ! Vous comprenez dès lors, qu'il n'est pas possible de ne pas tenir compte du circuit qui précède et du circuit qui suit le diviseur de tension. Mais en tenir compte ne veut pas dire pour autant que tout va devenir très compliqué. Il faut juste que la résistance globale R1 + R2 ait une valeur très supérieure à la résistance parasite RS de la source de tension, et que la valeur de R2 soit très inférieure à la valeur de la résistance d'entrée RE du circuit utilisateur. En même temps, il faut penser aux points suivants :
- le courant consommé par le pont diviseur doit être en relation avec la "capacité à fournir du courant" de la source de tension.
- choisir des valeurs très faibles pour les résistances n'est pas forcement compatible avec un système fonctionnant sur pile et devant avoir la plus grande autonomie possible.
- choisir des valeurs très élevées pour les résistances conduira à une consommation faible, mais l'influence du circuit utilisateur sera plus grande.
Sachant cela, vous devriez être capable de choisir en connaissance de cause les bonnes valeurs pour R1 et R2, sachant que les valeurs couremment utilisées tournent entre quelques centaines d'ohms et quelques centaines de KOhms.

Remarque importante : le pont diviseur résistif n'est pas toujours le moyen le mieux adapté pour obtenir une tension donnée, tout dépend du contexte d'utilisation. Il trouve sa place quand on veut une tension de sortie Vs qui conserve un certain rapport avec la tension d'entrée Ve. Un unique pont diviseur peut convenir pour fournir une tension de référence à quelques AOP (amplificateurs opérationnels), car l'impédance d'entrée des AOP est généralement très élevée et perturbe peu le pont diviseur. La fourniture d'une référence de tension à des convertisseurs analogique-numériques par exemple, ne peut pas se satisfaire d'un tel montage, où il faut avoir recours à une tension extrêmement stable qui ne peut être délivrée que par un régulateur de tension très précis.

Pont diviseur simple variable

L'utilisation d'un potentiomètre simple en remplacement des deux résistances d'un pont diviseur simple, permet de constituer un pont diviseur avec un rapport d'atténuation variable.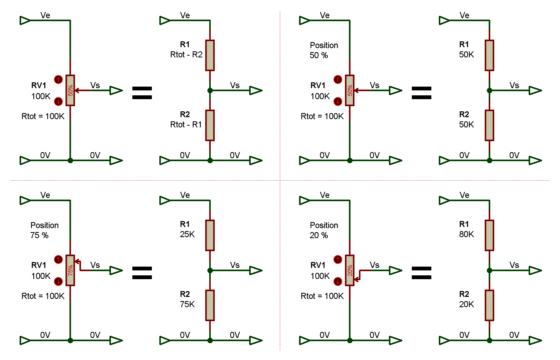



Sur les quatre quartiers du schéma ci-avant, la résistance R1 est matérialisée par la partie de piste résistive du potentiomètre qui est située entre l'extrémité reliée à Ve et le curseur. La résistance R2 quant à elle est matérialisée par la partie de piste résistive du potentiomètre qui est située entre l'extrémité reliée au 0V et le curseur. Si le curseur se déplace vers l'extremité 0V, la valeur de R1 augmente et la valeur de R2 diminue. Si le curseur se déplace vers l'extremité Ve, la valeur de R1 diminue et la valeur de R2 augmente.

Diviseur de tension multiple

Un diviseur de tension à deux résistances permet de délivrer une seule tension. Un diviseur de tension à trois résistances permet de délivrer deux tensions, selon le même principe que le diviseur de tension simple à deux résistances. Un diviseur de tension à quatre résistances permet de délivrer trois tensions. Etc, etc. Les formules permettant de déterminer les tensions de sorties d'un diviseur de tension à trois résistances, sont les suivantes :
Vs1 = Ve * (R3 / (R1 + R2 + R3))
Vs2 = Ve * ((R2 + R3) / (R1 + R2 + R3))

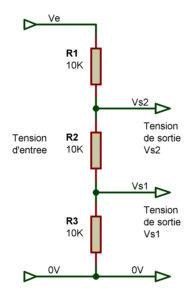Les trois résistances R1, R2 et R3 sont reliées en série, et on applique sur celles-ci, la tension d'entrée Ve. Si les résistances ont toutes la même valeur ohmique, ce qui est le cas sur ce schéma, elles vont s'approprier chacune la même portion de tension. Si Ve vaut 9.00V, chaque résistance aura 3.00V à ses bornes. Puis on "récupère" la tension disponible sur le couple R2 + R3 pour la tension de sortie Vs2, ou sur R3 seule pour la tension Vs1. Comme les trois résistances ont ici la même valeur, on récupère sur les sorties Vs1 et Vs2, des tensions ayant un rapport direct : 3.00V sur Vs1, et 6.00V sur Vs2. Valeurs théoriques, n'est-ce pas.

A quoi peut servir un pont diviseur à trois résistances ? A un contrôle fenêtré d'une tension, par exemple. Dans le montage pratique qui suit, les valeurs des résistances "parasites" (résistance interne de la source de tension et résistance d'entrée des circuits utilisateurs) ont repris des valeurs plus convenables et (pourtant) totalement réalistes.



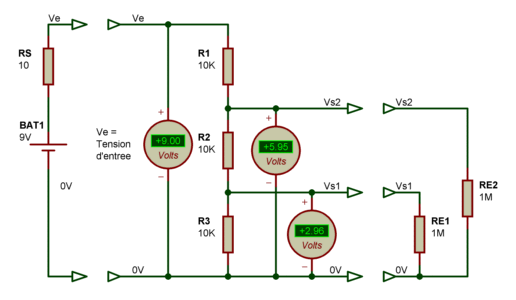
Et on constate, ma foi, que les tensions de sorties Vs1 et Vs2 que l'on mesure, sont tout de même bien proches des valeurs théoriques. 2.96V est proche de 3.00V, et 5.95V est très proche de 6.00V. Cela fait bien plaisir à voir et nous conforte dans l'hypothèse que l'on a pas travaillé pour rien. En bref, et pour résumer, nous pouvons compter sur un diviseur résistif pour fournir des tensions assez proches de celles recherchées, si l'environnement direct (avant et après le pont diviseur) est adapté.

Calcul des résistances pour un diviseur de tension simple

Cela est très simple. Nous connaissons la tension à diviser (c'est Ve) et nous connaissons la tension à obtenir (c'est Vs). La formule permettant de connaitre la tension de sortie en fonction de la valeur des résistances, est pour rappel, la suivante :
Vs = Ve * (R2 / (R1 + R2))
Il suffit de retourner cette formule pour non plus calculer la tension de sortie, mais pour calculer la valeur des résistances :
R2 = Vs * (R1 + R2) / Ve
R1 = (R1 + R2) - R2
Pour pouvoir exploiter ces formules, nous devons définir de façon arbitraire, la valeur ohmique totale obtenue par la somme des deux résistances montées en série, R1 + R2. Si on se souvient de ce qui a été dit tout à l'heure, on choisira cette valeur ohmique totale en fonction de ce qui précède et de ce qui suit le pont diviseur. Supposons que la source de tension Ve ait une résistance de sortie (interne) de 1 ohms, et que la résistance d'entrée du circuit utilisateur est de 400 Kohms. On peut sans trop de risque dire qu'une valeur ohmique totale de quelques 10 Kohms conviendra parfaitement. En partant de ce principe, on peut mettre en pratique la formule avec un exemple où la tension d'entrée Ve est de 6.8V, et où la tension de sortie désirée Vs est de 2.5V. Ce qui nous donne pour R1 et pour R2 , les valeurs suivantes :
R2 = 2.5 * 10000 / 6.8 = 3676
R1 = 10000 - 3676 = 6324

Reste à valider nos calculs :



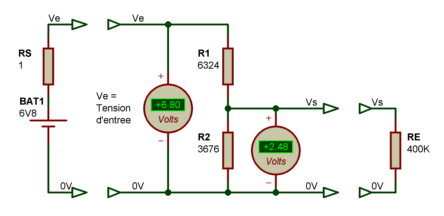
Nous trouvons 2.48V au lieu de 2.50V, et ce dans le contexte réel d'utilisation. Cela nous fait un écart de 0.02V, soit une erreur inférieure à 1%. Pas mal, non ?

Calcul des résistances pour un diviseur de tension multiple

Voilà une chose de faite. Maintenant, nous allons voir comment calculer les résistances d'un pont diviseur multiple pour obtenir 5 tensions de référence de 0.27V, de 0.55V, de 0.77V, de 1.10V et de 1.55V. Pourquoi ces valeurs précises ? Pour faire un vumètre à 5 leds avec seuils d'allumage à -12 dB, à -6 dB, à -3 dB, à 0 dB et à +3 dB (voir page Vumetre à leds - Conception). Cette fois, le calcul va se faire un peu différement, bien que le principe de base reste totalement le même : on décide d'une valeur ohmique globale pour l'ensemble des résistances mises en série, et on fixe la tension Ve. La valeur de cette tension Ve n'est pas critique, il faut simplement qu'elle soit supérieure à la tension de référence la plus élevée à obtenir. Dans le cas présent, la tension Ve doit être forcement supérieure à 1.55V, nous lui choisissons la valeur arbitraire de 2.50V. La résistance d'entrée des AOP que nous utilisons est de 2 Mohms. Nous pouvons fixer la valeur ohmique globale à 100K.
Le pont diviseur simple nous demande deux calculs, alors que le pont diviseur multiple à 5 tensions de sortie nous en demande plus. C'est plus en nombre, mais ce n'est pas plus en difficulté.

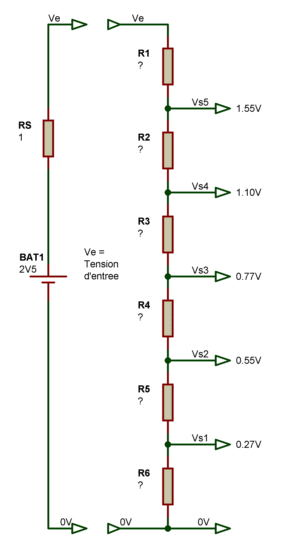Pour déterminer la valeur des 6 résistances R1 à R6 qui sont nécessaires pour obtenir les tensions désirées Vs1 à Vs5, nous allons procéder par étapes. La première consiste à considérer que les résistances R2 à R6 n'en forment qu'une seule, et à partir de là nous pouvons calculer R1, comme nous l'avons fait avant avec le pont diviseur simple. Une fois la valeur de R1 obtenue, et connaissant la valeur ohmique totale des 6 résistances, nous considèrerons le paquet R3 à R6 comme une seule résistance. Puis nous ferons de même pour les paquets R4 à R6, R5 et R6, et la résistance R6 viendra tout à la fin.

Pour simplifier les formules qui suivent, convenons des choses suivantes :
Rtot = R1 + R2 + R3 + R4 + R5 + R6 = 100K
Rtot / Ve = 100000 / 2.5 = 40000
Calculons la valeur de R1, pour obtenir notre tension de référence la plus élevée Vs5, égale à 2.18V. Une fois la valeur de R1 connue, calculons R2. Une fois la valeur de R2 connue, calculons R3, et ainsi de suite jusqu'à R6.
R1 = Rtot - (Vs5 * Rtot / Ve) = 100000 - (1.55 * 40000) = 38000
R2 = (Rtot - R1) - (Vs4 * Rtot / Ve) = 62000 -(1.10 * 40000) = 18000
R3 = (Rtot - R1 - R2) - Vs3 * Rtot / Ve) = 44000 - (0.77 * 40000) = 13200
R4 = (Rtot - R1 - R2 - R3) - (Vs2 * Rtot / Ve) = 30800 - (0.55 * 40000) = 8800
R5 = (Rtot - R1 - R2 - R3 - R4) - (Vs1 * Rtot / Ve) = 22000 - (0.27 * 44000) = 11200
R6 = (Rtot - R1 - R2 - R3 - R4 - R5) - (0 * Rtot / Ve) = 10800
Les valeurs de résistances ainsi calculées sont arrondies quand nécessaire, pour tomber sur des valeurs faciles à trouver dans les séries de valeurs normalisées courantes. Nous obtenons ainsi les valeurs de résistances suivantes :
R1 = 39K
R2 = 18K
R3 = 12K8
R4 = 9K1
R5 = 12K
R6 = 10K

Validation des calculs :

 

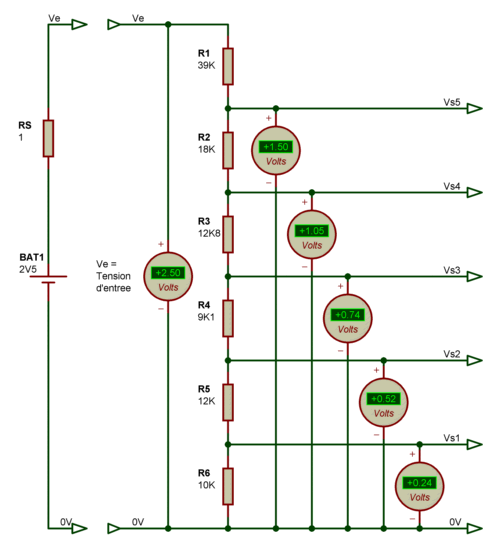
Erreurs faibles, cela me convient. J'espère qu'à vous aussi ;-).

Application 1 : convertisseur Température / Tension ou Lumière / Tension

Un pont diviseur constitué de deux résistances fixes fournit une tension qui est directement proportionnelle à la tension d'entrée. Il suffit de remplacer une des deux résistances par un composant dont la résistance varie en fonction de la température (CTN ou CTP par exemple), et nous avons là un convertisseur Température / Tension, qui délivre une tension proportionnelle à la température ambiante. Exemple d'une telle utilisation visible à la page Thermomètre 001. Et si vous remplacez une des deux résistances fixes par une élement sensible à la lumière (LDR par exemple), vous obtiendrez un convertisseur Lumière / Tension. Exemple d'une telle utilisation visible à la page Coeur clignotant.

Application 2 : Plusieurs calibres pour un voltmètre

La mise en pratique d'un pont diviseur multiple est sans doute sous votre nez, sans que vous le sachiez. Possédez-vous un multimètre ayant une fonction Voltmètre, avec un petit rotacteur permettant de choisir le calibre d'entrée 2V / 20V, 200V ? Oui ? Et bien voilà comment est conçu l'étage d'entrée de votre voltmètre.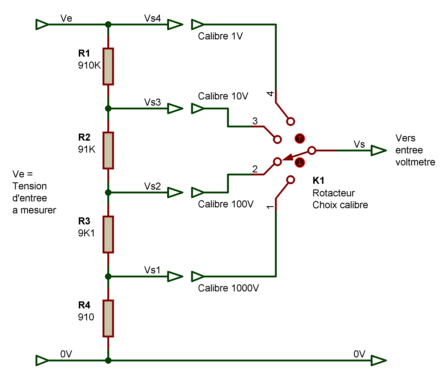



Sur cet exemple, les calibres sont de 1V, 10V, 100V et 1000V, car le diviseur a été conçu pour un voltmètre fait maison construit autour d'un CA3162 (convertisseur A/D) et CA3161 (décodeur BCD), qui permet d'afficher une tension continue comprise entre 0V et 999 mV. Si la tension à mesurer est inférieure à 1V, le rotacteur de sélection de calibre doit être placé en position 4. Si la tension à mesurer est comprise entre 1V et 10V, le rotacteur de sélection de calibre doit être placé en position 3. Les positions suivantes sont réservées pour les tensions d'entrée plus élevées.

Position Rotacteur	Tension de sortie Vs (voir Note 1)	Commentaire
Position 4 (1V)	Vs = Vs4 = Ve * (RA / RA) = Ve * 1	Aucun pont diviseur utilisé, aucune division. Si Ve = 0.5V, alors Vs = 0.5V.
Position 3 (10V)	Vs = Vs3 = Ve * (RB / RA) = Ve * 0,0999	Tension d'entrée divisée par 10. Si Ve = 5V, alors Vs = 0.5V.
Position 2 (100V)	Vs = Vs2 = Ve * (RC / RA) = Ve * 0,0099	Tension d'entrée divisée par 100. Si Ve = 50V, alors Vs = 0.5V.
Position 1 (1000V)	Vs = Vs1 = Ve * (RD / RA) = Ve * 0,0009	Tension d'entrée divisée par 1000. Si Ve = 500V, alors Vs = 0.5V.

Note 1 : Pour limiter la taille des formules dans le tableau, les valeurs RA, RB, RC et RD ont été attribuées à des groupes de résistances :
RA = R1 + R2 + R3 + R4
RB = R2 + R3 + R4
RC = R3 + R4
RD = R4