Sommaire | Services Pro | Musiques | Publications | Connectique | Electronique | Logiciels | Divers | Contacts | Liens | Glossaire | Historique

Electronique > Bases > Les effets spéciaux en audio > Delay (avec échantillonnage)

Dernière mise à jour : 27/08/2023

Présentation

Le présent article décrit les problématiques principales posées par l'échantillonnage d'un signal audio analogique en vue de produire un retard. Ces problématiques concernent aussi bien les systèmes analogiques que les systèmes numériques.
   

Delay

Delay = retard

Un effet audio appelé delay comporte une "ligne à retard" (delay line) dont le seul but est de décaler dans le temps un signal audio pour produire de façon artificielle un effet de réverbération ou d'écho. La ligne à retard peut être analogique ou numérique, et quand elle est analogique elle peut éventuellement mettre en oeuvre le principe de l'échantillonnage.

    bases_audio_effets_delay_principes_hl-sampling 
Les lignes à retard à BBD et les lignes à retard numériques utilisent toutes deux le principe de l'échantillonnage...
   
La qualité sonore du signal audio retardé dépend du type et des caractéristiques de la ligne à retard. Une ligne à retard numérique n'est pas forcément de meilleur qualité qu'une ligne à retard analogique.
   
Réverbération ou écho ?
Ces deux effets s'appuyent sur le principe du signal audio retardé, la différence principale réside dans le temps de retard, qui est bref pour l'effet de réverbération (< 60 ms) et long pour l'effet d'écho (> 60 ms). Si le temps qui sépare deux sons est très bref, le cerveau n'est pas capable de les discerner individuellement et a l'impression qu'ils sont "confondus" (d'où l'effet de résonnance). Si en revanche le temps qui sépare deux sons est assez long, alors le cerveau les perçoit de manière distincte et entend clairement les répétitions.

Remarque : il ne faut pas confondre "temps de retard" et "durée de l'effet". Le temps de retard correspond à l'intervale de temps qui sépare le moment où le son à retarder entre dans la ligne à retard et le moment où il en ressort. La durée de l'effet dépend bien sûr du temps de retard, mais aussi du nombre de fois où le signal retardé est réinjecté à l'entrée de la ligne à retard pour produire une nouvelle répétition. Si par exemple le temps de retard est de 50 ms et qu'il y a 20 répétitions - chacune subissant un retard de 50 ms par rapport à la précédente, alors la durée de l'effet sera de 1 seconde environ.

   

Delay analogique SANS échantillonnage

Le son peut se propager dans les solides, dans les liquides et dans les gaz. La vitesse de propagation du son dépend du milieu de transmission (solide, liquide ou gaz), en voici quelques exemples :

Si on parle devant une extrémité d'un tuyau en plastique de 100 mètres rempli d'air, le son sortira à l'autre extrémité du tuyau 0,3 seconde plus tard. Si un haut-parleur étanche diffuse de la musique dans l'eau d'une piscine, un plongeur immergé situé à 100 mètres du haut-parleur entendra la musique avec un retard de 0,06 seconde. Si enfin on s'arrange pour que du son transite dans une plaque métallique de 100 mètres de long, alors le retard sera de 0,02 seconde.

Avec les trois exemples donnés ci-devant, le son est transmis tel quel, sans discontinuité. La problématique principale posée par ces procédés est un temps de retard trop court pour obtenir un effet d'echo, ou quand cela est possible c'est en acceptant une très forte baisse de la qualité sonore. Autre point problématique : les dimensions physiques de la ligne à retard, car pour des délais très longs, il faut des longueurs ou surfaces très grandes. C'est sur ce point principalement que le procédé de retard avec échantillonnage présente un grand avantage.
   

Delay analogique AVEC échantillonnage

Le principe de l'échantillonnage repose sur la mesure ponctuelle et régulière d'un signal électrique, qui ici correspond au son sous sa forme électroacoustique (signal véhiculé dans un câble électrique). Le résultat de l'opération est un ensemble d'échantillons (un ensemble de mesures électriques de tension) dont la quantité par unité de temps détermine en grande partie la qualité du résultat et en particulier la bande passante maximale du système. Sans entrer dans les détails et d'après le théorème de Shannon/Nyquist, sachez qu'il faut au moins deux fois plus d'échantillons par seconde qu'il n'y a de périodes par seconde dans le signal sonore à retarder. Par exemple, si on veut pouvoir retarder un signal audio dont la fréquence est de 8000 Hz (8000 périodes par seconde), alors il faut au moins 16000 mesures pour disposer de 16000 échantillons.

Remarque : l'échantillonnage du son n'implique pas forcément une numérisation. Un échantillon peut très bien être stocké tel quel, sous sa forme analogique, dans des condensateurs qui jouent le rôle de réservoirs d'énergie. L'inconvénient avec cette méthode "toute analogique" est que la qualité sonore se dégrade vite quand on désire un temps de retard long, car dans ce cas il faut un très grand nombre de cellules de retard et chacune apporte une petite dégradation (problème bien connu des lignes à retard de type BBD telles les SAD1024 ou MN3011).

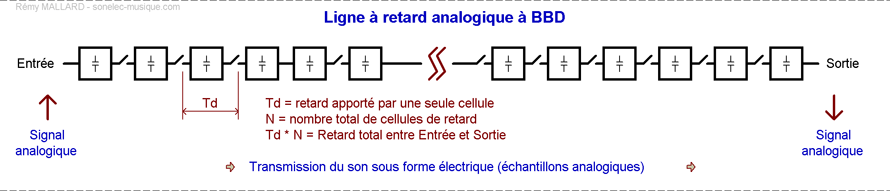
bases_audio_effets_delay_principes_sampling_analog 

Le nombre de cellules de retard conditionne le retard total maximal, mais aussi la qualité du signal retardé

   

Delay numérique (avec échantillonnage et numérisation)

Un delay numérique repose obligatoirement sur une phase d'acquisition du signal audio analogique (échantillonnage et numérisation), sauf bien sûr s'il s'agit d'un delay "tout numérique" doté uniquement d'une entrée numérique et d'une sortie numérique.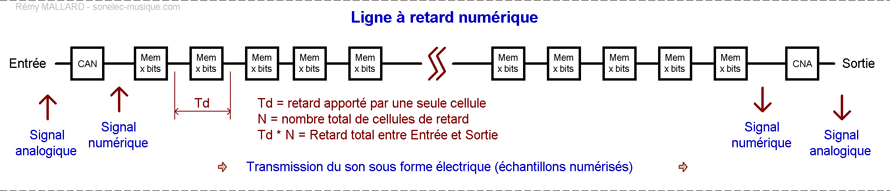

bases_audio_effets_delay_principes_sampling_digital
Le nombre de cellules de retard conditionne le retard total maximal, mais le signal retardé garde la même qualité quel que soit ce nombre

   

Paramètres d'échantillonnage, débit binaire et durée du retard

Pour qu'un signal audio qu'on numérise conserve une bonne qualité audio, les deux paramètres principaux de l'échantillonnage et de la numérisation doivent être "à la hauteur". Ces deux paramètres principaux sont les suivants :

La valeur choisie pour ces deux paramètres va directement influencer le débit binaire (exprimé en nombre de bits par seconde) et la durée du retard (exprimé en secondes).


Fréquence d'échantillonnage (en Hertz)
La fréquence d'échantillonnage correspond au nombre d'échantillons prélevés sur le signal audio analogique. D'après le théorème de Shannon/Nyquist, cette fréquence d'échantillonnage doit être supérieure au double de la fréquence maximale que l'on souhaite pouvoir traiter (et restituer). Cela a déjà été dit, mais il est bon de le répéter : dans le cas de figure où l'on souhaite traiter le son sur l'intégralité de la bande audio qui va de 20 Hz à 20000 Hz, la fréquence d'échantillonnage doit impérativement être supérieure à 40 kHz.

Résolution de la quantification (en nombre de bits)
La résolution correspond à la finesse de numérisation dans le sens "vertical " (amplitude) et est directement liée au nombre de bits de quantification. Si pour une application radiocom, téléphone ou anciens jeux vidéo on considère qu'une résolution de 8 bits suffisent, on considère en contrepartie qu'il faut au moins 16 bits pour une restitution sonore de haute fidélité. 
   
Débit binaire (en bits par seconde)
Le débit binaire correspond à la quantité d'éléments binaires (bits) traités en une seconde. Il dépend de la fréquence d'échantillonnage Fe (en Hertz) et de la résolution Q (en nombre de bits). Quelques exemples de débits binaires sont proposés dans le tableau qui suit.

Fréquence
échantillonnage
en Hertz		 Résolution
quantification
en nb de bits		 Débit binaire
en kilobits/sec
(1 kbps = 1000 bps)		 Débit binaire
en kilooctets/sec
(1 kBps = 1000 kBps)
8000 Hz 8 64000 bps = 64 Kbps 8000 Bps = 8 KBps
8000 Hz 16 128000 bps = 128 Kbps 16000 Bps = 16 KBps
22050 Hz 8 176400 bps =  176,4 Kbps 22050 Bps = 22,05 KBps
22050 Hz 16 352800 bps = 352,8 Kbps 44100 Bps =  44,1 KBps
44100 Hz 16 705600 bps = 705,6 Kbps 88200 Bps = 88,2 KBps
44100 Hz 24 1058400 bps = 1,0584 Mbps 132300 Bps = 132,3 KBps
48000 Hz 16 768000 bps = 768 Kbps 96000 Bps = 96 KBps
48000 Hz 24 1152000 bps = 1,152 Mbps 144000 Bps =  144 KBps
96000 Hz 24 2304000 bps = 2,304 Mbps 288000 Bps = 288 KBps

Remarque : l'unité "bps" avec un "b" minuscule signifie "bits per second", alors que l'unité "Bps" avec un "B" majuscule signifie "Bytes per second". Le terme "byte" qui signifie octet équivaut à 8 bits.

En quoi le débit binaire nous intéresse-t-il ici ? Ce paramètre est très important, car il conditionne le temps de retard maximal que l'on peut espérer avoir en fonction du nombre de cellules mémoire incluses dans la ligne à retard.

   
Durée maximale du retard en fonction du débit binaire
Prenons l'exemple d'un delay qui possède 1000 cellules mémoire, dans lesquelles on fait transiter des échantillons audio obtenus à une fréquence d'échantillonnage de 8 kHz et avec une résolution de 8 bits. Le débit binaire dans ces conditions est de 64 Kbps (8 KBps) et il nous faudrait donc 64000 cellules mémoire pour disposer d'un retard d'une seconde (8 kHz * 8 bits). En d'autre termes, le retard maximal avec 1000 cellules sera de seulement 1/64 de seconde (1000/64000), soit 15 ms. Ce temps de retard est suffisant pour créer un effet de réverbération, mais pas pour créer un effet d'écho.

Bien sûr, on pense immédiatement qu'une taille mémoire de 8 Ko (8 KB ou 64 Kb) n'est pas problématique, à une époque où on peut trouver des clés USB ou cartes SD de plusieurs dizaine de Go pour quelques euros. Malheureusement, ce type de mémoire ne convient pas dans le cas qui nous intéresse, car elle est trop lente (surtout pour la phase d'écriture qui peut atteindre plusieurs ms). Nous verrons ce point un peu plus loin. Pour l'instant, restons concentrés sur la durée possible du retard.

Nous avons vu qu'avec une mémoire de 8 Ko (et toujours pour une fréquence d'échantillonnage de 8 kHz et une résolution de 8 bits) on pouvait espérer un retard de 1 seconde. Malheureusement, adopter de tels paramètres produit un mauvais résultat sonore et s'il convient pour un répondeur/enregistreur, ce ne sera pas le cas pour un usage en studio. Pour ce dernier cas, il nous faut au moins 44 kHz de fréquence d'échantillonnage et 16 bits de résolution. Ce qui pour une durée de retard de 1 seconde conduit à un espace mémoire de 88 Ko (704 Kb). Et encore, on est en monophonie (espace mémoire à doubler si on veut traiter une source audio en stéréophonie). Là encore, on est en droit de penser qu'un tel espace mémoire de 88 Ko ne devrait pas poser de problème. Et dans les faits, on trouve en effet sur le marché des composants électroniques des mémoires de bonne taille à des prix raisonnables. A titre d'exemple, j'ai essayé avec succès des mémoires de 1Mb (128 Ko) et 2 Mb (256 Ko)... mais j'ai tout de même rencontré quelques difficultés qui seront évoquées ci-après.

   

Choix de la mémoire
Excluons tout de suite les mémoires de type EEPROM/Flash externes, car elles sont trop lentes. Il reste deux types de mémoire assez rapides qui sont les mémoires FRAM (mémoire ferromagnétique plutôt coûteuse) et SRAM (mémoire vive plus traditionnelle et moins coûteuse). Les types de mémoires avec lesquelles j'ai travaillé pour élaborer une chambre d'écho sont les suivantes :

Les deux mémoires externes FM25V20 et 23LC1024 peuvent être reliées à un microcontrôleur par une liaison SPI rapide (20 MHz) et leur temps d'écriture est très bref. Avec ces deux types de mémoire, j'ai pu atteindre une fréquence d'échantillonnage de 25 kHz avec un dsPIC cadencé à 80 MHz (voir delay 003). On a l'impression avec ces chiffres "faiblards" que quelque chose cloche, mais tout s'explique...

Premièrement, une liaison SPI est de type sérielle, ce qui signifie que tous les bits sont transmis à la queue-leu-leu, les uns après les autres. Pour un seul échantillon sonore, il faut trimballer 16 bits. Deuxièmement, il faut indiquer à la mémoire à quel endroit (à quelle adresse) on veut écrire ou lire, et cela occupe 24 bits. Troisièmement, il faut envoyer un ou plusieurs octets pour autoriser la phase d'écriture ou indiquee le mode de fonctionnement (en lecture ou écriture) désiré. Cela fait au minimum 48 bits à transmettre pour un seul échantillon de son. Et il n'y a pas que la mémoire externe qui engendre des données véhiculées en mode sériel. Il y a aussi le CAN (convertisseur analogique numérique) externe 16 bits et le CNA (convertisseur numérique analogique) externe 16 bits. En admettant qu'on ait 60 bits à transmettre en tout avec une fréquence d'horloge SPI de 5 MHz (période 0,2 us) cela réclame un temps de traitement d'au minimum 12 us. Et tout cela sans avoir pris en compte le temps de conversion du CAN qui peut atteindre plusieurs microsecondes et les indispensables temps d'attente entre diverses instructions dans le programme du microcontrôleur... Dans la pratique, il est difficile de faire beaucoup mieux que 40 us pour l'ensemble des traitements liés à un seul échantillon, ce qui nous ramène à une fréquence d'échantillonnage de 25 kHz.

Il faut tout de même que je précise que les longues durées de traitement pour les tests évoqués ci-devant résultent de contraintes techniques liées aux composants, mais aussi de choix techniques :

Voilà en résumé une petite réflexion sur la ou les méthodes à adopter en restant dans un domaine "amateur avancé". On peut, bien sûr, faire beaucoup mieux avec un microcontrôleur de haut de gamme ou un FPGA...